题目内容
14. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1.(1)求证:△DMN∽△BCN;
(2)求BD的长;
(3)若△DCN的面积为2,求四边形ABNM的面积.
分析 (1)由四边形ABCD为平行四边形,得到对边平行,即可证得:△DMN∽△BCN;
(2)由△DMN∽△BCN,可得到DN:BN=1:2,设OB=OD=x,表示出BN与DN,求出x的值,即可确定出BD的长;
(2)由相似三角形相似比为1:2,得到CN=2MN,BN=2DN.已知△DCN的面积,则由线段之比,得到△MND与△CNB的面积,从而得到S△ABD=S△BCD=S△BCN+S△CND,最后由S四边形ABNM=S△ABD-S△MND求解.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DMN=∠BCN,∠MDN=∠NBC,
∴△DMN∽△BCN;
(2)∵△DMN∽△BCN,
∴$\frac{MD}{CB}$=$\frac{DN}{BN}$,
∵M为AD中点,
∴MD=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
即$\frac{MD}{CB}$=$\frac{1}{2}$,
∴$\frac{DN}{BN}$=$\frac{1}{2}$,即BN=2DN,
设OB=OD=x,则有BD=2x,BN=OB+ON=x+1,DN=x-1,
∴x+1=2(x-1),
解得:x=3,
∴BD=2x=6;
(3)∵△MND∽△CNB,且相似比为1:2,
∴MN:CN=DN:BN=1:2,
∴S△MND=$\frac{1}{2}$S△CND=1,S△BNC=2S△CND=4.
∴S△ABD=S△BCD=S△BCN+S△CND=4+2=6,
∴S四边形ABNM=S△ABD-S△MND=6-1=5.
点评 此题考查了相似三角形的判定与性质以及平行四边形的性质.注意证得相似三角形的面积比等于相似比的平方,等高三角形面积的比等于其对应底的比.

练习册系列答案
相关题目
5.如图①,边长为a的大正方形中有四个边长均为b的小正方形,小华将阴影部分拼成了一个长方形(如图②),则这个长方形的面积为( )
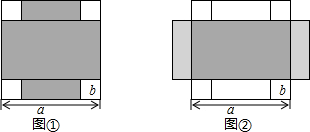

| A. | a2-4b2 | B. | (a+b)(a-b) | C. | (a+2b)(a-b) | D. | (a+b)(a-2b) |
4. 在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
 在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )
在如图所示的计算程序中,若输入x的值为-4.2,则输出的结果y为( )| A. | -4, | B. | 4 | C. | -5 | D. | 5 |
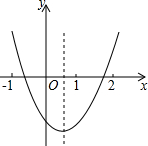 如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0,
如图,观察二次函数y=ax2+bx+c的图象,下列结论:①a+b+c>0,②2a+b>0, 沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论:
沿河岸有A,B,C三个港口,甲、乙两船同时分别从A,B港口出发,匀速驶向C港,最终到达C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.考察下列结论: