题目内容
8.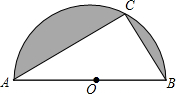 如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
如图,半圆的直径AB,点C在半圆上,已知半径为1,△ABC的周长为$\sqrt{5}$+2,则阴影部分的面积为$\frac{1}{2}π-\frac{1}{4}$.
分析 根据题意求出半圆的面积,根据完全平方公式求出△ABC的面积,根据阴影部分的面积=半圆的面积-△ABC的面积计算即可.
解答 解:∵圆的半径为1,
∴AB=2,半圆的面积=$\frac{1}{2}$×π×12=$\frac{1}{2}π$,
设AC=a,BC=b,
则a2+b2=4,a+b=$\sqrt{5}$,
∴2ab=1,
则$\frac{1}{2}$ab=$\frac{1}{4}$,
则阴影部分的面积为:$\frac{1}{2}π-\frac{1}{4}$,
故答案为:$\frac{1}{2}π-\frac{1}{4}$.
点评 本题扇形的相关计算,掌握扇形面积的计算公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
相关题目
19.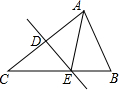 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
 如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )
如图,△ABC中,DE垂直平分AC,垂足为D,AD=3,△ABE的周长为13,那么△ABC的周长为( )| A. | 10 | B. | 13 | C. | 16 | D. | 19 |
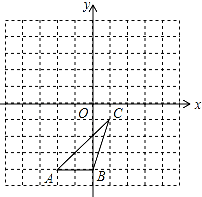 如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)
如图,△ABC各顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1)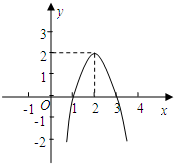 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答: