题目内容
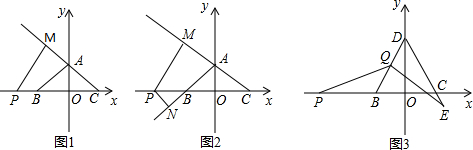
如图1,已知平面直角坐标系内,A(0,3),B(-4,0),C为x轴上正半轴上一点,若P为OB延长线上一点,PM⊥CA于M,且∠CPM=
∠BAC.
(1)求C点坐标;
(2)如图2,若OA2+OB2=AB2,过动点P向AB延长线作PN⊥AB于N,求证:PM-PN为定值;
(3)如图3,以BC为边作等边△BCD,Q为BD边的中点.连PQ,且∠PQE=120°.QE交DC延长线于E,问:在点P运动的过程中,CP-CE是否发生变化?若不变,求其值;若变化,请说明理由.
| 1 |
| 2 |
(1)求C点坐标;
(2)如图2,若OA2+OB2=AB2,过动点P向AB延长线作PN⊥AB于N,求证:PM-PN为定值;
(3)如图3,以BC为边作等边△BCD,Q为BD边的中点.连PQ,且∠PQE=120°.QE交DC延长线于E,问:在点P运动的过程中,CP-CE是否发生变化?若不变,求其值;若变化,请说明理由.

考点:全等三角形的判定与性质,坐标与图形性质,等边三角形的性质,勾股定理
专题:
分析:(1)根据同角的余角相等求出∠CPM=∠OAC,再求出∠OAB=∠OAC,再利用“角边角”证明△AOB和△AOC全等,根据全等三角形对应边相等可得OC=OB,然后写出点C的坐标即可;
(2)利用勾股定理列式求出AC,再利用三角函数用PC、PB表示出PM、PN,然后整理可得PM-PN=
BC;
(3)过点Q作QM⊥BC于M,作QN⊥CD于N,利用“角角边”证明△BQM和△DQN全等,根据全等三角形对应边相等可得QM=QN,BM=DN,再求出CM=CN,利用三角形的内角和定理求出∠QPM=∠E,然后利用“角角边”证明△PMQ和△ENQ全等,根据全等三角形对应边相等可得PM=NE,然后整理可得CP-CE=2MC.
(2)利用勾股定理列式求出AC,再利用三角函数用PC、PB表示出PM、PN,然后整理可得PM-PN=
| 3 |
| 5 |
(3)过点Q作QM⊥BC于M,作QN⊥CD于N,利用“角角边”证明△BQM和△DQN全等,根据全等三角形对应边相等可得QM=QN,BM=DN,再求出CM=CN,利用三角形的内角和定理求出∠QPM=∠E,然后利用“角角边”证明△PMQ和△ENQ全等,根据全等三角形对应边相等可得PM=NE,然后整理可得CP-CE=2MC.
解答:解:(1)∵PM⊥CA,
∴∠CPM+∠ACO=90°,
∵∠ACO+∠OAC=90°,
∴∠CPM=∠OAC,
又∵∠CPM=
∠BAC,
∴∠OAB=∠OAC,
在△AOB和△AOC中,
,
∴△AOB≌△AOC(ASA),
∴OC=OB=4,AB=AC,
∴点C(4,0);
(2)∵A(0,3),B(-4,0),
∴OA=3,OB=4,
由勾股定理得,AC=
=5,
∵AB=AC,
∴∠ACO=∠ABO,
∵∠PBN=∠ABO(对顶角相等),
∴∠PBN=∠ACO=∠ABO,
∴PM=PC•sin∠ACO=
PC,
PN=PB•sin∠ACO=
PB,
∴PM-PN=
PC-
PB=
BC=
×(4+4)=
,为定值;
(3)过点Q作QM⊥BC于M,作QN⊥CD于N,
∵△BCD是等边三角形,Q为BD边的中点,
∴∠CBD=∠BDC=60°,BQ=DQ,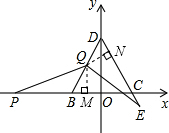
在△BQM和△DQN中,
,
∴△BQM≌△DQN(AAS),
∴QM=QN,BM=DN,
∴BC-BM=CD-DN,
即CM=CN,
∵∠PQE=120°,∠PCE=180°-60°=120°,
∴∠QPM=∠E,
在△PMQ和△ENQ中,
,
∴△PMQ≌△ENQ(AAS),
∴PM=NE,
∴CP-CE=(CM+PM)-CE=(CM+EN)-CE=(CM+CM+CE)-CE=2CM,
∵BC=4+4=8,点Q为BD的中点,
∴BQ=
×8=4,
∴BM=
×4=2,
∴CM=BC-BM=8-2=6,
∴CP-CE=2×6=12,为定值.
∴∠CPM+∠ACO=90°,
∵∠ACO+∠OAC=90°,
∴∠CPM=∠OAC,
又∵∠CPM=
| 1 |
| 2 |
∴∠OAB=∠OAC,
在△AOB和△AOC中,
|
∴△AOB≌△AOC(ASA),
∴OC=OB=4,AB=AC,
∴点C(4,0);
(2)∵A(0,3),B(-4,0),
∴OA=3,OB=4,
由勾股定理得,AC=
| 32+42 |
∵AB=AC,
∴∠ACO=∠ABO,
∵∠PBN=∠ABO(对顶角相等),
∴∠PBN=∠ACO=∠ABO,
∴PM=PC•sin∠ACO=
| 3 |
| 5 |
PN=PB•sin∠ACO=
| 3 |
| 5 |
∴PM-PN=
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 24 |
| 5 |
(3)过点Q作QM⊥BC于M,作QN⊥CD于N,
∵△BCD是等边三角形,Q为BD边的中点,
∴∠CBD=∠BDC=60°,BQ=DQ,

在△BQM和△DQN中,
|
∴△BQM≌△DQN(AAS),
∴QM=QN,BM=DN,
∴BC-BM=CD-DN,
即CM=CN,
∵∠PQE=120°,∠PCE=180°-60°=120°,
∴∠QPM=∠E,
在△PMQ和△ENQ中,
|
∴△PMQ≌△ENQ(AAS),
∴PM=NE,
∴CP-CE=(CM+PM)-CE=(CM+EN)-CE=(CM+CM+CE)-CE=2CM,
∵BC=4+4=8,点Q为BD的中点,
∴BQ=
| 1 |
| 2 |
∴BM=
| 1 |
| 2 |
∴CM=BC-BM=8-2=6,
∴CP-CE=2×6=12,为定值.
点评:本题考查了全等三角形的判定与性质,坐标与图形性质,等边三角形的性质,勾股定理,难点在于(3)作辅助线构造出全等三角形并二次证明三角形全等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF=
如图在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:BF= 已知一次函数y=-x+1与抛物线y=
已知一次函数y=-x+1与抛物线y= 已知AB=CD,BE=CF,AE=DF,问AB∥CD吗?
已知AB=CD,BE=CF,AE=DF,问AB∥CD吗?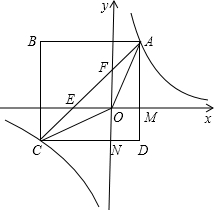 如图,矩形ABCD(点A在第一象限)与x轴的正半轴相交于M,与y的负半轴相交于N,AB∥x轴,反比例函数的图象y=
如图,矩形ABCD(点A在第一象限)与x轴的正半轴相交于M,与y的负半轴相交于N,AB∥x轴,反比例函数的图象y=