题目内容
9.下列运算正确的是( )| A. | $\frac{3a+b}{6}$=$\frac{a+b}{2}$ | B. | 2×$\frac{a+b}{3}$=$\frac{2a+b}{3}$ | C. | $\sqrt{{a}^{2}}$=a | D. | |a|=a(a≥0) |
分析 直接利用分式的基本性质以及绝对值的性质、二次根式的性质分别化简求出答案.
解答 解:A、$\frac{3a+b}{6}$无法化简,故此选项错误;
B、2×$\frac{a+b}{3}$=$\frac{2a+2b}{3}$,故此选项错误;
C、$\sqrt{{a}^{2}}$=|a|,故此选项错误;
D、|a|=a(a≥0),正确.
故选:D.
点评 此题主要考查了分式的基本性质以及绝对值的性质、二次根式的性质,正确掌握相关性质是解题关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
20.输入一组数据,按下列程序进行计算(x+8)2-826,输出结果如表:
分析表格中的数据,估计方程(x+8)2-826=0的一个正数解x的大致范围为( )
| x | 20.5 | 20.6 | 20.7 | 20.8 | 20.9 |
| 输出 | -13.75 | -8.04 | -2.31 | 3.44 | 9.21 |
| A. | 20.5<x<20.6 | B. | 20.6<x<20.7 | C. | 20.7<x<20.8 | D. | 20.8<x<20.9 |
17.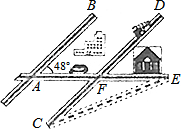 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
 某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )
某城市几条道路的位置关系如图所示,已知AB∥CD,AE与AB的夹角为48°,若CF与EF的长度相等,则∠C的度数为( )| A. | 48° | B. | 40° | C. | 30° | D. | 24° |
4.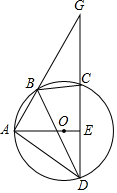 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )| A. | 50° | B. | 60° | C. | 80° | D. | 90° |
14.三角形的重心是( )
| A. | 三角形三条边上中线的交点 | B. | 三角形三条边上高线的交点 | ||
| C. | 三角形三条边垂直平分线的交点 | D. | 三角形三条内角平分线的交点 |
1.以下是关于正多边形的描述:
①正多边形的每条边都相等; ②正多边形都是轴对称图形;
③正多边形的外角和是360°;④正多边形都是中心对称图形.
其中正确的描述是( )
①正多边形的每条边都相等; ②正多边形都是轴对称图形;
③正多边形的外角和是360°;④正多边形都是中心对称图形.
其中正确的描述是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
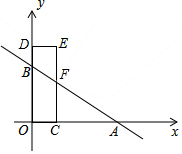 如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.
如图,在平面直角坐标系中,直线y=kx+b与x轴、y轴分别交于点A(6,0),B(0,3),点F为线段AB上任意一点,过点F作FC⊥OA于点C,延长CF至点E使EF=CF,作ED⊥y轴于点D.