题目内容
确定下列各式中m的值.
(1)(x+4)(x+9)=x2+mx+36;
(2)(x-2)(x-18)=x2+mx+36;
(3)(x+3)(x+p)=x2+mx+36;
(4)(x-6)(x-p)=x2+mx+36;
(5)(x+p)(x+q)=x2+mx+36,p、q为正整数.
(1)(x+4)(x+9)=x2+mx+36;
(2)(x-2)(x-18)=x2+mx+36;
(3)(x+3)(x+p)=x2+mx+36;
(4)(x-6)(x-p)=x2+mx+36;
(5)(x+p)(x+q)=x2+mx+36,p、q为正整数.
考点:多项式乘多项式
专题:计算题
分析:原式各项左边利用多项式乘以多项式法则计算,利用多项式相等的条件求出m的值即可.
解答:解:(1)(x+4)(x+9)=x2+13x+36=x2+mx+36,
解得:m=13;
(2)(x-2)(x-18)=x2-20x+36=x2+mx+36,
解得:m=-20;
(3)(x+3)(x+p)=x2+(p+3)x+3p=x2+mx+36,
∴p+3=m,3p=36,
解得:m=15,p=12;
(4)(x-6)(x-p)=x2-(p+6)x+6p=x2+mx+36,
∴-p-6=m,6p=36,
解得:m=-12,p=6;
(5)(x+p)(x+q)=x2+(p+q)x+pq=x2+mx+36,p、q为正整数,
∴p+q=m,pq=36,
当p=1,q=36时,m=37;当p=2,q=18时,m=20;当p=3,q=12时,m=15;当p=4,q=9时,m=13,
综上,m的值为37,20,15,13.
解得:m=13;
(2)(x-2)(x-18)=x2-20x+36=x2+mx+36,
解得:m=-20;
(3)(x+3)(x+p)=x2+(p+3)x+3p=x2+mx+36,
∴p+3=m,3p=36,
解得:m=15,p=12;
(4)(x-6)(x-p)=x2-(p+6)x+6p=x2+mx+36,
∴-p-6=m,6p=36,
解得:m=-12,p=6;
(5)(x+p)(x+q)=x2+(p+q)x+pq=x2+mx+36,p、q为正整数,
∴p+q=m,pq=36,
当p=1,q=36时,m=37;当p=2,q=18时,m=20;当p=3,q=12时,m=15;当p=4,q=9时,m=13,
综上,m的值为37,20,15,13.
点评:此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
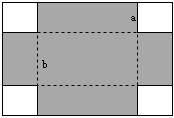 如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出补分折起,制成一个高为a的长方体形状的无盖纸盒,如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的长和宽.
如图,有一张长方形纸板,在它的四角各切去一个同样的正方形,然后将四周突出补分折起,制成一个高为a的长方体形状的无盖纸盒,如果纸盒的容积为4a2b,底面长方形的一边长为b(b<4a),求长方形纸板的长和宽.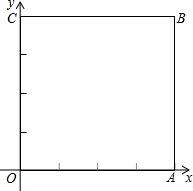 如图,已知正方形OABC的边长为4,请写出各个顶点的坐标.如果将它们的坐标同时缩小一半,得到一组新坐标,画出新坐标所对应的点,并把他们连接起来,得到一个新的图形,说出它的名称,你能说明其中的道理吗?
如图,已知正方形OABC的边长为4,请写出各个顶点的坐标.如果将它们的坐标同时缩小一半,得到一组新坐标,画出新坐标所对应的点,并把他们连接起来,得到一个新的图形,说出它的名称,你能说明其中的道理吗?