题目内容
已知直线AB上有一点O,射线OD和射线OC在AB的同侧,∠AOD=42°,∠BOC=34°,则∠AOD与∠BOC的平分线的夹角的度数是 .
考点:角的计算,角平分线的定义
专题:常规题型
分析:先求出∠COD,根据角平分线定义求出
∠AOD,
∠BOC即可解题.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:如图,

∵∠AOB=90°,∠AOD=42°,∠BOC=34°,
∴∠COD=180°-42°-34°=104°,
∠AOD与∠BOC的平分线的夹角的度数为
∠AOD+
∠BOC+∠COD=21°+17°+104°=142°.
故答案为142°

∵∠AOB=90°,∠AOD=42°,∠BOC=34°,
∴∠COD=180°-42°-34°=104°,
∠AOD与∠BOC的平分线的夹角的度数为
| 1 |
| 2 |
| 1 |
| 2 |
故答案为142°
点评:本题考查了角的平分线定义的应用,主要考查学生的计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.画出关于l成轴对称图形的△AB′C,五边形ACBB′C′的周长为
如图在长度为1个单位长度的小正方形组成的正方形中,点A,B,C在小正方形的顶点上.画出关于l成轴对称图形的△AB′C,五边形ACBB′C′的周长为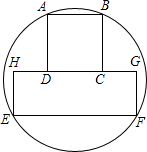 已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A,B,F,E四点,求该圆半径的长.
已知正方形ABCD和矩形EFGH按如图位置摆放,且AD=EH=2,EF=4,一圆过A,B,F,E四点,求该圆半径的长. 如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求
如图,在△ABC中,∠B=45°,∠C=30°,D是AC中点,DE⊥BC,求 (1)如图,已知点C在线段AB上,且AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长度.
(1)如图,已知点C在线段AB上,且AC=8cm,BC=6cm,点M、N分别是AC、BC的中点,求线段MN的长度.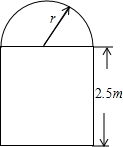 一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5米.如果隧道下部的宽度大于5米但不超过10米,求隧道横截面积S(平方米)关于上部半圆半径r(米)的函数解析式及函数的定义域.
一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为2.5米.如果隧道下部的宽度大于5米但不超过10米,求隧道横截面积S(平方米)关于上部半圆半径r(米)的函数解析式及函数的定义域.