题目内容
(1)先化简,再求值:
-
[
-a2+b2],其中a=3-2
,b=3
-3.
(2)
-
=
.
(3)
[
(
+1)-2]-x=1.
| 1 |
| 2a |
| 1 |
| a-b |
| a-b |
| 2a |
| 2 |
| 2 |
(2)
| 2 |
| 1+x |
| 3 |
| 1-x |
| 6 |
| x2-1 |
(3)
| 4 |
| 3 |
| 3 |
| 4 |
| x |
| 2 |
考点:分式的化简求值,解一元一次方程,解分式方程
专题:
分析:(1)先根据分式混合运算的法则把原式进行化简,再代入a,b进行计算即可.
(2)按解分式方程的方法计算求解.
(3)按解方程的方法计算即可.
(2)按解分式方程的方法计算求解.
(3)按解方程的方法计算即可.
解答:解(1)
-
[
-a2+b2]
=
-
[
-(a-b)(a+b)]
=
-
[(a-b)•
]
=
-
=
=a+b
∵a=3-2
,b=3
-3.
∴原式=a+b=3-2
+3
-3=
.
(2)
-
=
.
方程两边同时乘(1+x)(1-x)得
2(1-x)-3(1+x)=-6,
2-2x-3-3x=-6,
-5x=-5,
x=1,
把x=1代入(1+x)(1-x)=0
所以x=1是增根,原方程无解.
(3)
[
(
+1)-2]-x=1
×
(
+1)-
×2-x=1,
+1-
-x=1,
-
=
,
x=-
.
| 1 |
| 2a |
| 1 |
| a-b |
| a-b |
| 2a |
=
| 1 |
| 2a |
| 1 |
| a-b |
| a-b |
| 2a |
=
| 1 |
| 2a |
| 1 |
| a-b |
| 1-2a2-2ab |
| 2a |
=
| 1 |
| 2a |
| 1-2a2-2ab |
| 2a |
=
| 2a2+2ab |
| 2a |
=a+b
∵a=3-2
| 2 |
| 2 |
∴原式=a+b=3-2
| 2 |
| 2 |
| 2 |
(2)
| 2 |
| 1+x |
| 3 |
| 1-x |
| 6 |
| x2-1 |
方程两边同时乘(1+x)(1-x)得
2(1-x)-3(1+x)=-6,
2-2x-3-3x=-6,
-5x=-5,
x=1,
把x=1代入(1+x)(1-x)=0
所以x=1是增根,原方程无解.
(3)
| 4 |
| 3 |
| 3 |
| 4 |
| x |
| 2 |
| 4 |
| 3 |
| 3 |
| 4 |
| x |
| 2 |
| 4 |
| 3 |
| x |
| 2 |
| 8 |
| 3 |
-
| x |
| 2 |
| 8 |
| 3 |
x=-
| 16 |
| 3 |
点评:本题考查的是分式的化简求值,解分式方程及一元一次方程,熟悉解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
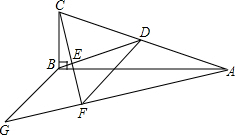 如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF
如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF 如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=110°,则∠2=
如图,直线AB与CD相交于E点,EF⊥AB,垂足为E,∠1=110°,则∠2=