题目内容
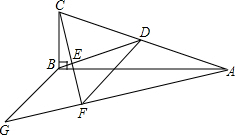 如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF
如图,在△ABC中,∠ABC=90°,D为AC的中点,过点C作CE⊥BD于点E,作∠GAB=∠CAB,CE的延长线与AG交于点F,点G在AF的延长线上,且FG=BD,连结BG、DF(1)求证:
①BD∥AG;
②四边形BGFD为菱形;
(2)已知AG=15,CF=3
| 7 |
考点:菱形的判定与性质
专题:
分析:(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;
(2)设GF=x,则AF=15-x,AC=2x,在Rt△ACF中利用勾股定理可求出x的值.
(2)设GF=x,则AF=15-x,AC=2x,在Rt△ACF中利用勾股定理可求出x的值.
解答:解:(1)①∵∠ABC=90°,D为AC的中点,
∴BD=AD=DC,
∴∠CAB=∠DBA,
∵∠GAB=∠CAB,
∴∠GAB=∠DBA,
∴AG∥BD;
②∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CE⊥BD,
∴CE⊥AG,
又∵BD为AC的中线,
∴BD=DF=
AC,
∴四边形BDFG是菱形;
(2)设GF=x,则AF=15-x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(15-x)2+(3
)2=(2x)2,
解得:x=6,
∴菱形BGFD的边长为6.
∴BD=AD=DC,
∴∠CAB=∠DBA,
∵∠GAB=∠CAB,
∴∠GAB=∠DBA,
∴AG∥BD;
②∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CE⊥BD,
∴CE⊥AG,
又∵BD为AC的中线,
∴BD=DF=
| 1 |
| 2 |
∴四边形BDFG是菱形;
(2)设GF=x,则AF=15-x,AC=2x,
∵在Rt△ACF中,∠CFA=90°,
∴AF2+CF2=AC2,即(15-x)2+(3
| 7 |
解得:x=6,
∴菱形BGFD的边长为6.
点评:本题考查了菱形的判定与性质、勾股定理及直角三角形的斜边中线的性质,解答本题的关键是判断出四边形BGFD是菱形.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
 (1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2.
(1)先化简,再求值:(a-2)(a+2)+3(a+2)2-6a(a+2),其中a=2. 如图,已知点O是△ABC的两条角平分线的交点.
如图,已知点O是△ABC的两条角平分线的交点. 如图,已知a∥b,∠1=50°,则∠2的度数为
如图,已知a∥b,∠1=50°,则∠2的度数为