题目内容
19．如果两个相似三角形的对应中线比是$\sqrt{3}$：2，那么它们的周长比是$\sqrt{3}$：2．分析 直接根据相似三角形的性质即可得出结论．
解答 解：∵两个相似三角形的对应中线比是$\sqrt{3}$：2，
∴它们的周长比为$\sqrt{3}$：2．
故答案为：$\sqrt{3}$：2．
点评 本题考查的是相似三角形的性质，熟知相似三角形的对应线段（对应中线、对应角平分线、对应边上的高）的比等于相似比是解答此题的关键．
练习册系列答案
相关题目
如图，△ABC中，MP垂直平分AB，QN垂直平分AC，若AB=3，AC=6，BC=8，求△APQ的周长．
如图，边长为x的正方形中有两个半圆形
7．多项式-x2-$\frac{1}{2}$x-1的次数和项数分别是（ ）
| A． | 3，2 | B． | 2，3 | C． | 2，2 | D． | 3，3 |
14．一飞机从距离地面3000米的高空测得一地面监测点的俯角是60°，那么此时飞机与监测点的距离是（ ）
| A． | 6000米 | B． | 1000$\sqrt{3}$米 | C． | 2000$\sqrt{3}$米 | D． | 3000$\sqrt{3}$米 |
11．
如图，在?ABCD中，点E是边BA延长线上的一点，CE交AD于点F．下列各式中，错误的是（ ）
如图，在?ABCD中，点E是边BA延长线上的一点，CE交AD于点F．下列各式中，错误的是（ ）| A． | $\frac{AE}{AB}=\frac{FE}{FC}$ | B． | $\frac{AE}{AB}=\frac{AF}{DF}$ | C． | $\frac{AE}{AB}=\frac{AF}{BC}$ | D． | $\frac{AE}{BE}=\frac{AF}{BC}$ |
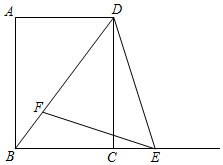如图，已知四边形ABCD是矩形，cot∠ADB=$\frac{3}{4}$，AB=16．点E在射线BC上，点F在线段BD上，且∠DEF=∠ADB．