题目内容
14．一飞机从距离地面3000米的高空测得一地面监测点的俯角是60°，那么此时飞机与监测点的距离是（ ）| A． | 6000米 | B． | 1000$\sqrt{3}$米 | C． | 2000$\sqrt{3}$米 | D． | 3000$\sqrt{3}$米 |
分析 根据题意可构造直角三角形，利用所给角的正弦函数即可求解．
解答 解：如图所示：
由题意得，∠CAB=60°，BC=3000米，
在Rt△ABC中，∵sin∠A=$\frac{BC}{AC}$，
∴AC=$\frac{BC}{sinA}$=$\frac{3000}{\frac{\sqrt{3}}{2}}$=2000$\sqrt{3}$米．
故选C．
点评 本题考查了解直角三角形的应用，解答本题的关键是借助俯角构造直角三角形，并结合三角函数解直角三角形．
练习册系列答案
通城学典默写能手系列答案
相关题目
4．某商场经营某种品牌的玩具，购进时的单价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每上涨1元，就会少售出10件玩具．
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
（2）在第（1）问的条件下，若商场获得了8750元销售利润，求该玩具销售单价x应定为多少元？
（3）在第（1）问的条件下，若玩具厂规定该品牌玩具销售单价不低于32元，且商场要完成不少于400件的销售任务，求：商场销售该品牌玩具获得最大利润是多少？
（1）不妨设该种品牌玩具的销售单价为x元（x＞30），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：
| 销售单价（元） | x（x＞30） |
| 销售量y（件） | -10x+800 |
| 销售玩具获得利润w（元） | -10x2+1000x-16000 |
（3）在第（1）问的条件下，若玩具厂规定该品牌玩具销售单价不低于32元，且商场要完成不少于400件的销售任务，求：商场销售该品牌玩具获得最大利润是多少？
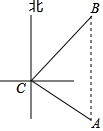如图，一艘海轮位于小岛C的南偏东60°方向，距离小岛120海里的A处，该海轮从A处正北方向航行一段距离后，到达位于小岛C北偏东45°方向的B处．
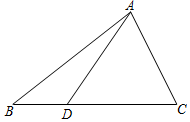如图，已知点D是△ABC的边BC上一点，且BD=$\frac{1}{2}$CD，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$．
4．下列多项式中，在实数范围不能分解因式的是（ ）
| A． | x2+y2+2x+2y | B． | x2+y2+2xy-2 | C． | x2-y2+4x+4y | D． | x2-y2+4y-4 |