��Ŀ����
��ͼ,OPΪ��AOB�Ľ�ƽ����,PC��OA,PD��OB,����ֱ���C��D,�����н��۴�����ǣ� ��
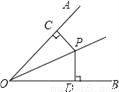
A. PC=PD B. ��CPD=��DOP C. ��CPO=��DPO D. OC=OD
 B
�������������������֪OPΪ��AOB�Ľ�ƽ���ߣ�PC��OA��PD��OB������ֱ���C��D�����ݽ�ƽ���ߵ����ʿɵ�PC=PD��A��ȷ����Rt��OCP��Rt��ODP�У�OP=OP,PC=PD����HL���ж���OCP�ա�ODP������ȫ�������ε����ʿɵá�CPO=��DPO��OC=OD����C��D��ȷ�����ܵó���CPD=��DOP����B���ʴ�ѡB��
B
�������������������֪OPΪ��AOB�Ľ�ƽ���ߣ�PC��OA��PD��OB������ֱ���C��D�����ݽ�ƽ���ߵ����ʿɵ�PC=PD��A��ȷ����Rt��OCP��Rt��ODP�У�OP=OP,PC=PD����HL���ж���OCP�ա�ODP������ȫ�������ε����ʿɵá�CPO=��DPO��OC=OD����C��D��ȷ�����ܵó���CPD=��DOP����B���ʴ�ѡB��
 �¿α�������������ҵ�������γ�����ϵ�д�
�¿α�������������ҵ�������γ�����ϵ�д� ����ν����Ž̲��㽭���̴�ѧ������ϵ�д�
����ν����Ž̲��㽭���̴�ѧ������ϵ�д� �����Ļ������������������ϵ�д�
�����Ļ������������������ϵ�д���һ�������ΰ�����Ҫ����4��:
(1)�ָ�������ͼ�α�������Գ�ͼ��;
(2)���ֵõ�4��ͼ����ȫ��ͼ��.
���㰴����������Ҫ��,�ֱ���ͼ��,��,���е��������л���3�ֲ�ͬ�ķָ��.(��д����)
 �𰸲�Ψһ,
���������ָ�������ͼ�α�������Գ�ͼ�Σ������ߵ��д��ߣ��Ŀ�ͼ�ε���ȫ��ͬ�������϶࣬����Ҫ�ɣ�
��������
��ͼ��ʾ.
�𰸲�Ψһ,
���������ָ�������ͼ�α�������Գ�ͼ�Σ������ߵ��д��ߣ��Ŀ�ͼ�ε���ȫ��ͬ�������϶࣬����Ҫ�ɣ�
��������
��ͼ��ʾ. �����AΪ��ǣ���sinA��0.6����ô��������
A. 0�㣼A��30�� B. 30�㣼A��45��
C. 45�㣼A��60�� D. 60�㣼A��90��
 B
����������sin30��="1/2," sin45��=,<0.6<
��30�㣼��A��45�㣬��ѡB
B
����������sin30��="1/2," sin45��=,<0.6<
��30�㣼��A��45�㣬��ѡB �ס�����������ͬ��·�ߴ�A��B������ʻ��A��B���ؼ��·��Ϊ20 km�������н���·��s(km)��ס��ҳ�����ʱ��t(h)֮���ϵ��ͼ����ͼ��ʾ������ͼ����Ϣ������˵����ȷ����( )
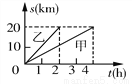
A. ���ٶ���4 km/h B. �ҵ��ٶ���10 km/h C. �ұȼ�������1 h D. �ױ�������B��3 h
 B
��������A. ���ٶ���20��4=5 km/h���ʲ���ȷ��
B. �ҵ��ٶ���20��2=10 km/h������ȷ��
C. ��ͼ��֪���Һͼ�ͬʱ�������ʲ���ȷ��
D. ��ͼ��֪���ױ�������B��2 h���ʲ���ȷ��
��ѡB.
B
��������A. ���ٶ���20��4=5 km/h���ʲ���ȷ��
B. �ҵ��ٶ���20��2=10 km/h������ȷ��
C. ��ͼ��֪���Һͼ�ͬʱ�������ʲ���ȷ��
D. ��ͼ��֪���ױ�������B��2 h���ʲ���ȷ��
��ѡB. ��ͼ��һ������ABCD��AD��BC���ֽ������²������Ե�BΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�BA��BC�ڵ�G��H���ٷֱ��Ե�G��HΪԲ�ģ�����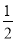 GH�ij�Ϊ�뾶�����������ڡ�ABC�ڲ��ཻ�ڵ�O��������BO����AD�ڵ�E��
GH�ij�Ϊ�뾶�����������ڡ�ABC�ڲ��ཻ�ڵ�O��������BO����AD�ڵ�E��
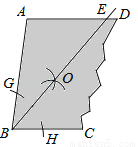
��1����֤��AB=AE��
��2������A=100�㣬���EBC�Ķ�����
 ��1��֤���������������2��40�㣮
�������������������1���ɽ�ƽ���ߵ����ʣ����Եõ���AEB=��EBC���ɽ�ƽ���ߵ����ʣ��õ���EBC=��ABE���ɵ��������ε��ж����ɵô𰸣�
��2���������ε��ڽǺͶ������ɵá�AEB����ƽ���ߵ����ʣ��ɵô𰸣�
�����������1����AD��BC�����AEB=��EBC���� BE�ǡ�ABC�Ľ�ƽ���ߣ����EBC=��ABE�����AEB=��ABE����A...
��1��֤���������������2��40�㣮
�������������������1���ɽ�ƽ���ߵ����ʣ����Եõ���AEB=��EBC���ɽ�ƽ���ߵ����ʣ��õ���EBC=��ABE���ɵ��������ε��ж����ɵô𰸣�
��2���������ε��ڽǺͶ������ɵá�AEB����ƽ���ߵ����ʣ��ɵô𰸣�
�����������1����AD��BC�����AEB=��EBC���� BE�ǡ�ABC�Ľ�ƽ���ߣ����EBC=��ABE�����AEB=��ABE����A... ��ͼ��ʾ����һ�����г��IJ���ʾ��ͼ����֪����ֱ��Ϊ65 cm��������AC�ij�Ϊ42 cm������AE�ij�Ϊ18 cm����E��A��C��ͬһ��ֱ���ϣ���������B����������C����ֱ��BC�����ƽ�У���C��73�㣬����E������ľ���EF��(�����ȷ��l cm���ο����ݣ�sin 73���0.96��cos 73���0.29��tan 73���3.27)
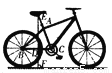
 90
�������������������ͼ��ʾ�����������߶���EF����DF=0.5��65=32.5Ϊ��֪������ֻ�����ED����ED��ֱ��������ECD�У��ҡ�C=73��Ϊ��֪��б��EC=60Ϊ��֪�����Կ������ҵĸ������ED=60��sin73���60��0.96��57.6���ټ���32.5��EF�ij�ԼΪ90cm��
�����������ͼ����Rt��EDC�У�
CE=AE��AC=18��42=60(cm)��
...
90
�������������������ͼ��ʾ�����������߶���EF����DF=0.5��65=32.5Ϊ��֪������ֻ�����ED����ED��ֱ��������ECD�У��ҡ�C=73��Ϊ��֪��б��EC=60Ϊ��֪�����Կ������ҵĸ������ED=60��sin73���60��0.96��57.6���ټ���32.5��EF�ij�ԼΪ90cm��
�����������ͼ����Rt��EDC�У�
CE=AE��AC=18��42=60(cm)��
... ��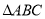 ��
�� 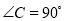 ��
�� 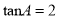 ����
����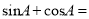 _______ ��
_______ ��
 �������������������ͼ��
��tanA=2��
����AB=x����BC=2x��
AC= ��
����sinA+cosA=��
�ʴ�Ϊ�� ��
�������������������ͼ��
��tanA=2��
����AB=x����BC=2x��
AC= ��
����sinA+cosA=��
�ʴ�Ϊ�� �� ��ͼ���ڡ�ABC�У���D��BC�ϣ�AB=AD=DC����B=80�㣬���C�Ķ���Ϊ��������

A. 30�� B. 40�� C. 45�� D. 60��
 B
������������������ȸ��ݵ��������ε����������ADB�Ķ���������ƽ�ǵĶ���ó���ADC�Ķ��������ݵ��������ε����ʼ��ɵó����ۣ�
��������
�ߡ�ABD�У�AB=AD����B=80�㣬
���B=��ADB=80�㣬
���ADC=180�㩁��ADB=100�㣬
��AD=CD��
���C===40�㣮
��ѡ��B��
B
������������������ȸ��ݵ��������ε����������ADB�Ķ���������ƽ�ǵĶ���ó���ADC�Ķ��������ݵ��������ε����ʼ��ɵó����ۣ�
��������
�ߡ�ABD�У�AB=AD����B=80�㣬
���B=��ADB=80�㣬
���ADC=180�㩁��ADB=100�㣬
��AD=CD��
���C===40�㣮
��ѡ��B�� С����Ͷ�����ڵ���Ϸ���������һ����ͼ��ʾ�İ��ӣ���E��F�ֱ��Ǿ���ABCD������AD��BC�ϵĵ㣬EF��AB����M��N��EF���������㣬��Ͷ��һ�Σ�����������Ӱ���ֵĸ�����(����)

A.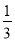 B.
B.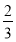 C.
C.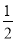 D.
D.
 C
�����������ı���ABFE����Ӱ������������ı���ABFE������ı���DCFE����Ӱ������������ı���DCFE�����
����Ӱ���ֵ������������ABCD�������
�����������Ӱ���ֵĸ�����.
C
�����������ı���ABFE����Ӱ������������ı���ABFE������ı���DCFE����Ӱ������������ı���DCFE�����
����Ӱ���ֵ������������ABCD�������
�����������Ӱ���ֵĸ�����. 
