题目内容
如图所示，BA⊥CA，AB∥CD，AB＝CE，AC＝CD，则△ABC≌______，理由是_____，所以∠ABC＝______，∠ACB＝______，由此可知BC与DE的位置关系为__________.
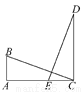
△CED SAS ∠CED ∠CDE 互相垂直
【解析】∵BA⊥CA，
∴∠BAC=90°，
∵AB∥CD，
∴∠ACD=∠BAC=90°，
在△ACB和△CDE中，
，
∴△ABC≌△ECD(SAS),
∴∠ABC＝∠CED，∠ACB＝∠CDE，
又因∠ACB+∠BCD=90°，
∴∠CDE+∠BCD=90°，
∴BC⊥DE.
...
练习册系列答案
相关题目
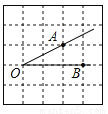
如图，将∠AOB放在边长为1的小正方形组成的网格中，则tan∠AOB= ．
．
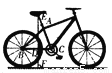
【解析】试题分析：过点A作AD⊥OB垂足为D，如图，在直角△ABD中，AD=1，OD=2，则tan∠AOB==．故答案为： ． 如图所示的是一辆自行车的侧面示意图．已知车轮直径为65 cm，车架中AC的长为42 cm，座杆AE的长为18 cm，点E，A，C在同一条直线上，后轴轴心B与中轴轴心C所在直线BC与地面平行，∠C＝73°，求车座E到地面的距离EF．(结果精确到l cm，参考数据：sin 73°≈0.96，cos 73°≈0.29，tan 73°≈3.27)
90
【解析】试题分析：如图所示，题中所求线段是EF，而DF=0.5×65=32.5为已知，所以只需求出ED，而ED在直角三角形ECD中，且∠C=73°为已知，斜边EC=60为已知，所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6，再加上32.5即EF的长约为90cm．
试题解析：如图，在Rt△EDC中，
CE=AE＋AC=18＋42=60(cm)．
... 在△ABC中，AB＝AC，且BC＝8cm，BD是腰AC的中线，△ABC的周长分为两部分，已知它们的差为2cm，则等腰三角形的腰长为__________.
10cm或6cm
【解析】如图∵BD是腰AC的中线，
∴AD=CD，
①当△ABD的周长与△BCD的周长差为2时，即AB+AD+BD-(BD+BC+CD)=2,
∴AB-BC=2,
∵BC=8cm，
∴AB=10cm.
②当△BCD的周长与△ABD的周长差为2时，即BD+BC+CD -(AB+AD+BD)=2,
∴BC - AB =2,
∵BC... 如图，在△ABC中，点D在BC上，AB=AD=DC，∠B=80°，则∠C的度数为（ ）
A. 30° B. 40° C. 45° D. 60°
B
【解析】试题分析：先根据等腰三角形的性质求出∠ADB的度数，再由平角的定义得出∠ADC的度数，根据等腰三角形的性质即可得出结论．
【解析】
∵△ABD中，AB=AD，∠B=80°，
∴∠B=∠ADB=80°，
∴∠ADC=180°﹣∠ADB=100°，
∵AD=CD，
∴∠C===40°．
故选：B． 在等腰△ABC中，∠A=30°，AB=8，则AB边上的高CD的长是 ．
4或或。
【解析】根据题意画出AB=AC，AB=BC和AC=BC时的图象，然后根据等腰三角形的性质和解直角三角形，分别进行计算即可：
(1)如图，
当AB=AC时，
∵∠A=30°，
∴CD=AC=×8=4。
（2）如图，当AB=BC时，
则∠A=∠ACB=30°。
∴∠ACD=60°。∴∠BCD=30°
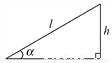
∴CD=cos∠BCD•BC=cos3... 如图，某游乐场一山顶滑梯的高为h，滑梯的坡角为α，那么滑梯长l为( )
A.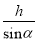 
B. 
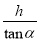C.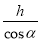 
D. h·sinα
A
【解析】根据锐角三角函数的定义可得，sinα= ，即可得l=，故选A. 小明家里的阳台地面,水平铺设着仅黑白颜色不同的18块方砖(如图),他从房间里向阳台抛小皮球,小皮球最终随机停留在某块方砖上.
(1)求小皮球分别停留在黑色方砖与白色方砖上的概率.
(2)(1)中哪个概率较大?要使这两个概率相等,应改变哪块方砖的颜色?
（1）， (2)小皮球停留在黑色方砖上的概率大.
【解析】试题分析：（1）根据小球停在黑色方砖上的概率就是黑色方砖面积与总面积的比值，小球停在白色方砖上的概率就是白色方砖面积与总面积的比值，再根据黑色方砖、白色方砖的个数与总个数之间的关系，即可求出答案；
（2）要想这两个概率相等，只要使黑色方砖的个数与白色方砖的个数相等即可．
试题解析：【解析】
（1）∵白色方砖8块，黑色方砖... 已知△ABC≌△DEF，若AB=5，BC=6，AC=8，则△DEF的周长是( )
A. 8 B. 18
C. 19 D. 20
C
【解析】试题解析：∵AB=5，BC=6，AC=8，
∴△ABC的周长=AB+BC+AC=5+6+8=19，
∵△ABC≌△DEF，
∴△DEF的周长等于△ABC的周长，
∴△DEF的周长是19.
故选C.