题目内容
6.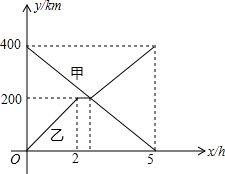 甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲、乙两辆汽车分别从A、B两地同时出发,沿同一条公路相向而行,乙车车发2h后休息,与甲车相遇后,继续行驶,设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:(1)求:y甲与x的函数关系式,并写出自变量x的取值范围;
(2)乙车休息了0.5h;
(3)当两车相距80km时,直接写出x的值.
分析 (1)由函数图象和待定系数法得出解析式;
(2)由图象把y=200代入甲的解析式中得出两车相遇的时间,进而得出乙车休息的时间;
(3)分两种情况讨论,当0≤x≤2.5时,2.5<x≤5时,由路程=速度×时间就可以得出结论.
解答 (1)解:设y甲=kx+b,根据题意,得
$\left\{\begin{array}{l}{400=b}\\{0=5k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-80}\\{b=400}\end{array}\right.$
所以y甲=-80x+400;
自变量x的取值范围是0≤x≤5.
(2)由图象把y=200代入甲的解析式中可得:200=-80x+400,
解得:x=2.5,
所以乙车休息了2.5-2=0.5,
故答案为:0.5;
(3)当0≤x≤2.5时,可得:100x+80=-80x+400
解得:x=$\frac{16}{9}$;
当2.5<x≤5时,80x-80=-80x+400,
解得:x=3;
当两车相距80km时,x的值为$\frac{16}{9}$或3.
点评 本题考查了行程问题的数量关系的运用,分段函数的运用,解答时认真分析函数的图象的意义,充分理解函数图象所表示的数量关系是关键.

练习册系列答案
相关题目
17.八(1)班组织了一次汉字听写比赛,甲、乙两队各10人,其比赛成绩如下表(10分制):
(1)甲队成绩的中位数是9分,乙队成绩的众数是10分.
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
| 甲队 | 7 | 8 | 9 | 10 | 10 | 10 | 10 | 9 | 9 | 8 |
| 乙队 | 7 | 7 | 8 | 9 | 10 | 10 | 9 | 10 | 10 | 10 |
(2)计算甲队的平均成绩和方差.
(3)已知乙队成绩的方差是1.4,则成绩较为整齐的是甲队.
1.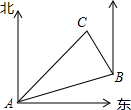 同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
 同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )
同学甲要从A点出发到距离A点1000米的C地去,他先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了600米到达目的地C,由此可知AB之间的距离为( )| A. | 700米 | B. | 700$\sqrt{3}$米 | C. | 800米 | D. | 800$\sqrt{3}$米 |
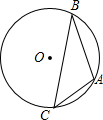 已知:如图,A,B,C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长.
已知:如图,A,B,C为⊙O上的三个点,⊙O的直径为4cm,∠ACB=45°,求AB的长. 已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数.
已知:如图,直线m∥n.Rt△ABC与直线m、n分别相交,且∠1=25°,∠2=80°,求∠A的度数. 如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).
如图,利用一面足够长的墙,用铁栅栏围成一个矩形自行车场地ABCD,在AB和BC边各有一个2米宽的小门(不用铁栅栏),设矩形ABCD的宽AD为x米,矩形的长为AB(且AB>AD).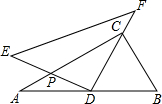 将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.
将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.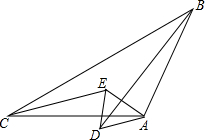 如图,△ABC与△ADE中,AB=AC,AD=AE,∠BAC+∠DAE=180°,试判断△ACE与△ABD面积之间的关系,并说明理由.
如图,△ABC与△ADE中,AB=AC,AD=AE,∠BAC+∠DAE=180°,试判断△ACE与△ABD面积之间的关系,并说明理由.