题目内容
19.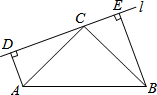 如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
如图,在Rt△ABC中,∠ACB=90°,AC=BC,过C点作直线l,点 D,E在直线l上,连接AD,BE,∠ADC=∠CEB=90°.求证:△ADC≌△CEB.
分析 先证明∠DAC=∠ECB,根据AAS证△ADC≌△CEB.
解答 证明:∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=CB}\end{array}\right.$,
∴△ADC≌△CEB(AAS).
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
7. 如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
 如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在平行四边形ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
14.菱形具有而矩形不一定具有的性质是( )
| A. | 对角相等 | B. | 每条对角线平分一组对角 | ||
| C. | 对角线互相平分 | D. | 对边平行且相等 |
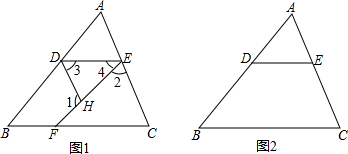 如图1,△ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C.
如图1,△ABC中,D,E,F三点分别在AB,AC,BC三边上,过点D的直线与线段EF的交点为点H,∠1+∠2=180°,∠3=∠C. 如图,PA、PB切⊙O于A、B两点,且切线长PA=5,CD切⊙O于点E,分别交PA、PB于点C、D,则△PCD的周长为10.
如图,PA、PB切⊙O于A、B两点,且切线长PA=5,CD切⊙O于点E,分别交PA、PB于点C、D,则△PCD的周长为10. 如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab.
如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作四边形A1B1C1D1,然后再以四边形A1B1C1D1各边的中点为顶点作四边形A2B2C2D2,…,如此下去,可得到四边形A2014B2014C2014D2014,它的面积用含a,b的代数式表示为$\frac{1}{{2}^{2015}}$ab. 在?ABCD中,∠A比∠B大30°,求∠C的度数.
在?ABCD中,∠A比∠B大30°,求∠C的度数.