题目内容
20．在△ABC中，∠A，∠B都是锐角，且sinA=$\frac{1}{2}$，cosB=$\frac{\sqrt{3}}{2}$，则△ABC是（ ）| A． | 直角三角形 | B． | 钝角三角形 | C． | 锐角三角形 | D． | 等边三角形 |
分析 先根据题意得出∠A，∠B的值，再由三角形内角和定理求出∠C的度数，进而可得出结论．
解答 解：∵在△ABC中，∠A，∠B都是锐角，且sinA=$\frac{1}{2}$，cosB=$\frac{\sqrt{3}}{2}$，
∴∠A=30°，∠B=30°，
∴∠C=180°-30°-30°=120°，
∴△ABC是钝角三角形．
故选B．
点评 本题考查的是特殊角的三角函数值，熟记各特殊角度的三角函数值是解答此题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10．对于正比例函数y=2x，下列判断正确的是（ ）
| A． | 自变量x的值毎增加1，函数y的值增加2 | |
| B． | 自变量x的值毎增加1，函数y的值减少2 | |
| C． | 自变量x的值毎增加1，函数y的值增加$\frac{1}{2}$ | |
| D． | 自变量x的值毎增加1，函数y的值减少$\frac{1}{2}$ |
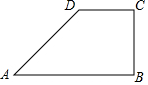如图，四边形ABCD中，AB||CD，BC⊥AB；AD=5，CD=3，BC=4．