题目内容
11.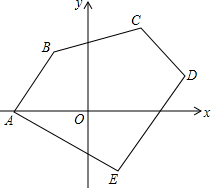 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
分析 作BF⊥x轴于点F,CG⊥x轴于点G,DI⊥x轴于点I,作EH⊥DI的延长线于点H,五边形ABCDE的面积=△ABF面积+梯形BFGC的面积+梯形CGID的面积+梯形AEHI的面积-三角形DEH的面积,由此求得答案即可.
解答 解:如图,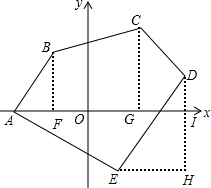
∵A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),
∴BF=4,AF=3,FG=6,CG=5,GI=2,DI=2,AI=11,HE=4,DH=6,HI=4,
∴五边形ABCDE的面积=△ABF面积+梯形BFGC的面积+梯形CGID的面积+梯形AEHI的面积-三角形DEH的面积
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×(4+5)×6+$\frac{1}{2}$×(5+2)×2+$\frac{1}{2}$×(4+11)×4-$\frac{1}{2}$×4×6
=6+27+7+30-12
=58.
点评 本题考查了坐标与图形,解决本题的关键是不规则多边形的面积的求解利用规则图形的面积的和与差求解.

练习册系列答案
相关题目
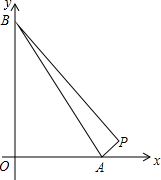 由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢?
由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢? 如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于40,则BC=13.
如图,在△ABC中,已知AC=27,AB的垂直平分线交AB于点D,交AC于点E,△BCE的周长等于40,则BC=13.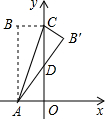 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$). 如图所示,△ABC中,AD为中线,且△ABC的面积为5,则△ACD的面积为$\frac{5}{2}$.
如图所示,△ABC中,AD为中线,且△ABC的面积为5,则△ACD的面积为$\frac{5}{2}$.