题目内容
6.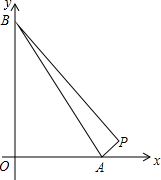 由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢?
由点P(14,1),A(a,0),B(0,a)(0<a<14),确定的△PAB的面积为18,求a的值.如果a>14呢?
分析 当0<a<14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可;
当a>14时,作PD⊥x轴于点D,由P(14,1),A(a,0),B(0,a)就可以表示出△ABP的面积,建立关于a的方程求出其解即可.
解答 解:当0<a<14时,
如图,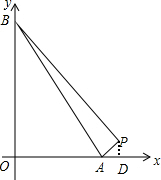
作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S梯形OBPD-S△OAB-S△ADP=$\frac{1}{2}$×14(a+1)-$\frac{1}{2}$a2-$\frac{1}{2}$×1×(14-a)=18,
解得:a1=3,a2=12;
当a>14时,如图,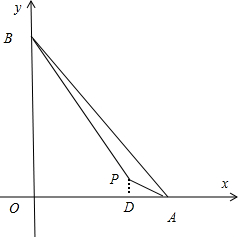
作PD⊥x轴于点D,
∵P(14,1),A(a,0),B(0,a),
∴PD=1,OD=14,OA=a,OB=a,
∴S△PAB=S△OAB-S梯形OBPD-S△ADP=$\frac{1}{2}$a2-$\frac{1}{2}$×14(a+1)-$\frac{1}{2}$×1×(a-14)=18,
解得:a1=$\frac{15+3\sqrt{41}}{2}$,a2=$\frac{15-3\sqrt{41}}{2}$(不合题意,舍去);
∴a=$\frac{15+3\sqrt{41}}{2}$.
点评 本题考查了坐标与图形的性质,三角形的面积公式的运用,梯形的面积公式的运用,点的坐标的运用,解答时运用三角形和梯形的面积建立方程求解是关键.

练习册系列答案
相关题目
14.设sin48°=a,cos24°=b,tan46°=c,不使用计算器(不查表)可知,下列关系式中,正确的是( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
1.如图所示,四边形ABCD是平行四边形,按下列条件得到的四边形BFDE是平行四边形的个数是( )

①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.

①图甲,DE⊥AC,BF⊥AC
②图乙,DE平分∠ADC,BF平分∠ABC
③图丙,E是AB的中点,F是CD的中点
④图丁,E是AB上一点,EF⊥AB.
| A. | 3个 | B. | 4个 | C. | 1个 | D. | 2个 |
16.若等腰三角形的底边长为6cm,一腰上的中线把它的周长分成差为2cm的两部分,则腰长为( )
| A. | 4cm | B. | 8cm | C. | 4cm或8cm | D. | 以上都不对 |
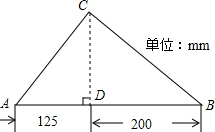 一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标.
一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标.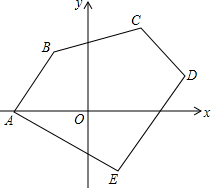 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.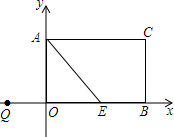 如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.
如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.