题目内容
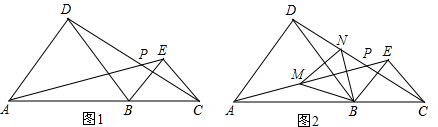
1. 如图所示,△ABC中,AD为中线,且△ABC的面积为5,则△ACD的面积为$\frac{5}{2}$.
如图所示,△ABC中,AD为中线,且△ABC的面积为5,则△ACD的面积为$\frac{5}{2}$.
分析 根据等底等高的三角形的面积相等可知三角形的中线把三角形分成面积相等的两个三角形解答.
解答  解:∵如图所示,△ABC中,AD为中线,
解:∵如图所示,△ABC中,AD为中线,
∴S△ACD=$\frac{1}{2}$S△ABC.
又∵△ABC的面积为5,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{5}{2}$.
故答案是:$\frac{5}{2}$.
点评 本题考查了三角形的面积,熟记三角形的中线把三角形分成面积相等的两个三角形是解题的关键.

练习册系列答案
相关题目
12.若|a|=5,|b|=3,那么a•b的值是( )
| A. | 15 | B. | -15 | C. | ±15 | D. | 以上都不对 |
9.将方程x2+8x+9=0左边配方后,正确的是( )
| A. | (x+4)2=-9 | B. | (x+4)2=25 | C. | (x+4)2=7 | D. | (x+4)2=-7 |
16.若等腰三角形的底边长为6cm,一腰上的中线把它的周长分成差为2cm的两部分,则腰长为( )
| A. | 4cm | B. | 8cm | C. | 4cm或8cm | D. | 以上都不对 |
11.下列式子正确的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | $\sqrt{196}=±$14 | C. | $\sqrt{(-13)^{2}}$=13 | D. | -$\sqrt{14.4}$=-1.2 |
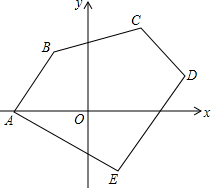 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.