题目内容
3.正数a的正的平方根叫做a的算术平方根,记作:$\sqrt{a}$,我们把$\sqrt{a}$≥0和a≥0叫做$\sqrt{a}$的两个非负性,据此解决以下问题:(1)若实数a、b满足$\sqrt{a-1}+\sqrt{(9+b)^{2}}$=0,求a+b的立方根.
(2)已知实数x、y满足y=$\sqrt{x-2}$+$\sqrt{2-x}$+2,求xy的平方根.
分析 (1)根据非负数的性质求出a、b的值,根据立方根的概念求出答案;
(2)根据算术平方根的非负性求出x、y的值,根据平方根的概念解答.
解答 解:(1)由题意得a-1=0,9+b=0,
解得a=1,b=-9,
∴a+b=-8,
∴a+b的立方根是-2;
(2)由题意得,x-2≥0,2-x≤0,
解得x=2,
则y=2,
xy的平方根是±2.
点评 本题考查的是非负数的性质,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
10.将(x2+x)2-14(x2+x)+24分式因解,正确的是( )
| A. | (x2+x-12)(x2+x-2) | B. | (x2+x-6)(x2+x-4) | C. | (x+4)(x-3)(x+2)(x-1) | D. | (x-4)(x+3)(x-2)(x+1) |
8.下列事件中,属于必然事件的是( )
| A. | 在地面向上空跑石块,石块终将落下 | |
| B. | 有一匹马以70米/秒的速度奔跑 | |
| C. | 杭州明年五一节当天的最高气温35℃ | |
| D. | 射击运动员射击一次,命中10环 |
12.若|a|=5,|b|=3,那么a•b的值是( )
| A. | 15 | B. | -15 | C. | ±15 | D. | 以上都不对 |
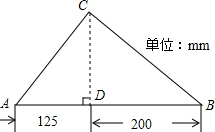 一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标.
一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标.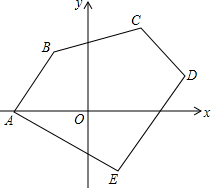 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.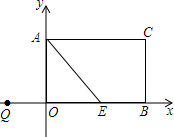 如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.
如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.