题目内容
20.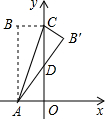 如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
如图,矩形ABCO中,OA在x轴上,OC在y轴上,且OA=2,AB=5,把△ABC沿着AC对折得到△AB′C,AB′交y轴于D点,则B′点的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
分析 作B′E⊥x轴,设OD=x,在Rt△AOD中,根据勾股定理列方程,可求得D点的坐标,然后依据△ADO∽△AB′E可求得B′E、AE的长,从而可求得点B′的坐标.
解答 解:作B′E⊥x轴,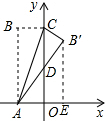
∵∠BAC=∠B′AC,∠BAC=∠OCA,
∴∠B′AC=∠OCA,
∴AD=CD,
设OD=x,AD=5-x,
在Rt△AOD中,根据勾股定理列方程得:22+x2=(5-x)2,
解得:x=2.1,
∴OD=2.1.
∴AD=CD=5-2.1=2.9.
∵CO⊥AO,B′E⊥AO,
∴DO∥B′E.
∴△ADO∽△AB′E.
∴$\frac{AD}{AB′}=\frac{OD}{B′E}=\frac{AO}{AE}$,即$\frac{2.9}{5}=\frac{2.1}{B′E}=\frac{2}{AE}$.
解得:B′E=$\frac{105}{29}$,AE=$\frac{100}{29}$.
∴OE=$\frac{42}{29}$.
∴点B′的坐标为($\frac{42}{29}$,$\frac{105}{29}$).
故答案为:($\frac{42}{29}$,$\frac{105}{29}$).
点评 本题主要考查的是翻折的性质、勾股定理的应用、相似三角形的性质和判定,求得点D的坐标是解题的关键.

练习册系列答案
相关题目
8.下列事件中,属于必然事件的是( )
| A. | 在地面向上空跑石块,石块终将落下 | |
| B. | 有一匹马以70米/秒的速度奔跑 | |
| C. | 杭州明年五一节当天的最高气温35℃ | |
| D. | 射击运动员射击一次,命中10环 |
12.若|a|=5,|b|=3,那么a•b的值是( )
| A. | 15 | B. | -15 | C. | ±15 | D. | 以上都不对 |
9.将方程x2+8x+9=0左边配方后,正确的是( )
| A. | (x+4)2=-9 | B. | (x+4)2=25 | C. | (x+4)2=7 | D. | (x+4)2=-7 |
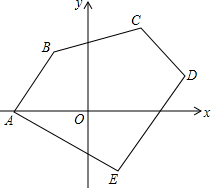 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.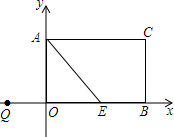 如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.
如图,矩形AOBC,A(0,3)、B(5,0),点E在OB上,∠AEO=45°,点P从点Q(-3,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t (t≥0)秒.