题目内容
19.当n是正整数时,因为(n+1)2>n(n+2)所以有$\frac{n}{n+1}$<$\frac{n+1}{n+2}$,参考这个结论,比较A=$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$与B=$\frac{1}{10}$的大小A<B.分析 根据题意可得,$\frac{1}{2}<\frac{2}{3}$,$\frac{5}{6}<\frac{6}{7}$,…,将式子两个一组进行比较,依此继续下去,就可以得到$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$<$\frac{2}{3}×\frac{4}{5}×\frac{6}{7}×$…×$\frac{98}{99}$,最后两边同时乘以$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$得到问题的答案.
解答 解:∵A=$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$
∴A=$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$<$\frac{2}{3}×\frac{4}{5}×\frac{6}{7}×$…×$\frac{98}{99}$
∴($\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$)×($\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$)<($\frac{2}{3}×\frac{3}{4}$)×$(\frac{6}{7}×\frac{7}{8})$×…×$(\frac{98}{99}×\frac{99}{100})$=$\frac{1}{100}$,
∴$\frac{1}{2}$×$\frac{3}{4}$×$\frac{5}{6}$×…×$\frac{99}{100}$<$\frac{1}{10}$,
∴A<B.
点评 本题考查对分式乘法的掌握,关键是找出规律,进行化简.

(1)填写下表并判断物体在哪下落得快?地球
| t | 0 | 2 | 4 | 6 | 8 | 10 |
| h=4.9t2 | 0 | 19.6 | 78.4 | 176.4 | 313.6 | 490 |
| H=0.8t2 | 0 | 3.2 | 12.8 | 28.8 | 51.2 | 80 |
| A. | 在地面向上空跑石块,石块终将落下 | |
| B. | 有一匹马以70米/秒的速度奔跑 | |
| C. | 杭州明年五一节当天的最高气温35℃ | |
| D. | 射击运动员射击一次,命中10环 |
| A. | (x+4)2=-9 | B. | (x+4)2=25 | C. | (x+4)2=7 | D. | (x+4)2=-7 |
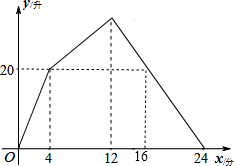 某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示
某容器装有一个进水管和三个相同的出水管,从某时刻开始的4分钟内只进水不出水,在随口的8分钟内在进水的同时开放一个出水管出水.每分钟单个进水管和出水管的进、出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)的关系如图所示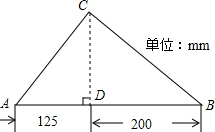 一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标.
一个三角形的形状和尺寸如图所示,已知∠B=45°,建立适当的直角坐标系,在坐标系中作出这个三角形,并标出各顶点的坐标. 如图,一张四边形纸片ABCD中,AB∥CD,把它剪一刀,然后拼成一个三角形,要求说明你的剪法和原理,并画出示意图.
如图,一张四边形纸片ABCD中,AB∥CD,把它剪一刀,然后拼成一个三角形,要求说明你的剪法和原理,并画出示意图.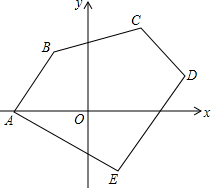 在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.
在平面直角坐标系中,已知:A(-5,0)、B(-2,4)、C(4,5)、D(6,2)、E(2,-4),求五边形ABCDE的面积.