题目内容
9.请你估计一下$\frac{({2}^{2}-1)({3}^{2}-1)({4}^{2}-1)…(201{5}^{2}-1)(201{6}^{2}-1)}{{1}^{2}•{2}^{2}•{3}^{2}•{4}^{2}…201{5}^{2}•201{6}^{2}}$的值应该最接近于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{2015}$ |
分析 利用平方差公式$\frac{{n}^{2}-1}{{n}^{2}}$=$\frac{(n+1)(n-1)}{{n}^{2}}$,对所求式子进行化简,从而进行求解.
解答 解:∵$\frac{{n}^{2}-1}{{n}^{2}}$=$\frac{(n+1)(n-1)}{{n}^{2}}$,
∴原式=$\frac{3×1}{{2}^{2}}$×$\frac{2×4}{{3}^{2}}$×$\frac{3×5}{{4}^{2}}$×…×$\frac{2015×2017}{201{6}^{2}}$=$\frac{1}{2}$×$\frac{2017}{2016}$
∴$\frac{({2}^{2}-1)({3}^{2}-1)({4}^{2}-1)…(201{5}^{2}-1)(201{6}^{2}-1)}{{1}^{2}•{2}^{2}•{3}^{2}•{4}^{2}…201{5}^{2}•201{6}^{2}}$的值应该最接近于$\frac{1}{2}$.
故选:B.
点评 此题主要考查平方差公式的性质及其应用,解题的关键是利用平方差公式进行展开.

练习册系列答案
相关题目
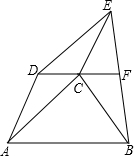 已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.
已知:如图,梯形ABCD,AB∥CD,以AC、AD为边向外作?ACED,联结BE,点F是BE的中点,联结CF.求证:CF∥AB.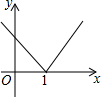
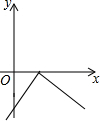
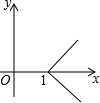
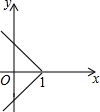
 请根据如图所示的已知条件,求出抛物线解析式,并写出顶点坐标.
请根据如图所示的已知条件,求出抛物线解析式,并写出顶点坐标.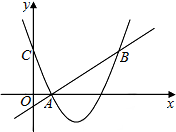 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.