题目内容
20.△ABC中,AB=10,AC=8,则BC边上的中线AD的取值范围是( )| A. | 8<AD<10 | B. | 2<AD<18 | C. | 4<AD<5 | D. | 1<AD<9 |
分析 延长AD至E,使DE=AD,连接CE.根据SAS证明△ABD≌△ECD,得CE=AB,再根据三角形的三边关系即可求解.
解答 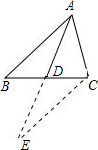 解:延长AD至E,使DE=AD,连接CE.
解:延长AD至E,使DE=AD,连接CE.
∵BD=CD,∠ADB=∠EDC,AD=DE,
∴△ABD≌△ECD,
∴CE=AB.
在△ACE中,CE-AC<AE<CE+AC,
即2<2AD<18,
1<AD<9.
故选:D.
点评 此题考查了全等三角形的判定和性质、三角形的三边关系.注意:倍长中线是常见的辅助线之一.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
12.“十•一”黄金周期间,一农家花博园统计了10月1日至10月6日每天参观的人数及变化,如表(正数表示比前一天多的人数,负数表示比前一天少的人数):
(1)若10月1日的游客人数记为a人,请用a的代数式表示10月3日的游客人数(直接在横线上写出结果):a+450.
(2)若a=1000,花博园门票每人20元,问10月1日至6日期间游客人数最多一天门票收入多少元?
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 |
| 人数 | a | -100 | +550 | -200 | +600 | -300 |
(2)若a=1000,花博园门票每人20元,问10月1日至6日期间游客人数最多一天门票收入多少元?
9.如图,若数轴上的两点A、B表示的数分别为a、b,则下列结论正确的是( )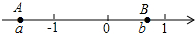
| A. | a+b<0 | B. | a-b>0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
10.下列各式计算正确的是( )
| A. | 6a+a=7a2 | B. | -2a+5b=3ab | C. | 4m2n-2mn2=2mn | D. | 3ab2-5b2a=-2ab2 |
 如图为抛物线y=ax2+bx+c,则4a-2b+c=0(值).
如图为抛物线y=ax2+bx+c,则4a-2b+c=0(值).
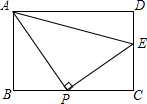 如图,在矩形ABCD中,AB=3,AD=4,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.
如图,在矩形ABCD中,AB=3,AD=4,P是BC上的任意一点(P与B、C不重合),过点P作AP⊥PE,垂足为P,PE交CD于点E.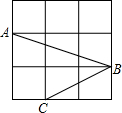 如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.
如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.