如图.网格中的每个小正方形的边长都是1.A.B.C三点是小正方形的顶点.则∠ABC的度数为45°．题目和参考答案——青夏教育精英家教网—

题目内容

5．

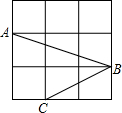如图，网格中的每个小正方形的边长都是1，A，B，C三点是小正方形的顶点，则∠ABC的度数为45°．

分析连接AC，利用勾股定理的逆定理证明△ACB为直角三角形即可得到∠ABC的度数．

解答解：连接AC，

由勾股定理得：AC=BC=$\sqrt{5}$，AB=$\sqrt{10}$，
∵AC²+BC²=AB²=10，
∴△ABC为等腰直角三角形，
∴∠ABC=45°．
故答案为：45°．

点评本题考查了勾股定理的知识，解答本题的关键是根据正方形的性质求出边长，在格点三角形中利用勾股定理．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a²+b²=c²
证明：连接DB，过点D作BC边上的高DF，
则DF=EC=b-A．
∵S_{四边形ADCB}=S_△ACD+S_△ABC=$\frac{1}{2}$b²+$\frac{1}{2}$ab．
又∵S_{四边形ADCB}=S_△ADB+S_△DCB=$\frac{1}{2}$c²+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}$b²+$\frac{1}{2}$ab=$\frac{1}{2}$c²+$\frac{1}{2}$a（b-a）
∴a²+b²=c²
请参照上述证法，利用图2完成下面的证明：
将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．
求证：a²+b²=c²．
证明：连结BD
∵S_{多边形ACBED}=$\frac{1}{2}ab$+$\frac{1}{2}$b²+$\frac{1}{2}$ab
又∵S_{多边形ACBED}=$\frac{1}{2}$ab+$\frac{1}{2}$c²+$\frac{1}{2}$a（b-a）
∴$\frac{1}{2}ab$+$\frac{1}{2}$b²+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c²+$\frac{1}{2}$a（b-a）
∴a²+b²=c²．

16．某城市5年前人均年收入为n元，预计今年人均年收入是5年前的2倍多800元，则今年人均年收入将达（2n+800）元．

13．关于x的方程x²+mx-20=0的一个根是4，则另一个根是-5，m=1．

20．△ABC中，AB=10，AC=8，则BC边上的中线AD的取值范围是（　　）

10．（1）化简：4x-5-3（x-2）；
（2）先化简，再求值：x²y+5xy-3（2x²y+xy），其中x=-$\frac{1}{2}$，y=4．

17．$\sqrt{144}$的平方根是（　　）

14．

15．

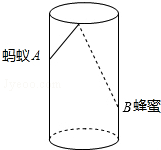如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处到达内壁B处的最短距离为（　　）

试题分类