题目内容
15.已知点D在△ABC的边BC上(不与B、C重合),AB<BC,连结AD,要使△ABD与△ABC相似,应添加的一个条件是∠BAD=∠C或∠BDA=∠BAC或$\frac{AB}{BC}=\frac{BD}{AB}$(写出一种即可).分析 由于△ABD与△ABC有公共角∠B,若根据有两组角对应相等的两个三角形相似,可添加∠BAD=∠C或∠BDA=∠BAC;若根据两组对应边的比相等且夹角对应相等的两个三角形相似,则可添加$\frac{AB}{BC}$=$\frac{BD}{AB}$.
解答 解: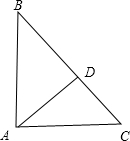 ∵∠ABD=∠CBA,
∵∠ABD=∠CBA,
∴当∠BAD=∠C时,△BAD∽△BCA;
当∠BDA=∠BAC时,△BAD∽△BCA;
当$\frac{AB}{BC}$=$\frac{BD}{AB}$时,△BAD∽△BCA.
故答案为∠BAD=∠C或∠BDA=∠BAC或$\frac{AB}{BC}$=$\frac{BD}{AB}$.
故答案为∠BAD=∠C或∠BDA=∠BAC或$\frac{AB}{BC}$=$\frac{BD}{AB}$.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.

练习册系列答案
相关题目
3.一个正多边形的每个外角都等于36°,那么它是( )
| A. | 正五边形 | B. | 正六边形 | C. | 正八边形 | D. | 正十边形 |
20.△ABC中,AB=10,AC=8,则BC边上的中线AD的取值范围是( )
| A. | 8<AD<10 | B. | 2<AD<18 | C. | 4<AD<5 | D. | 1<AD<9 |
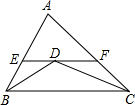 如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于点D,过D作直线平行于BC,交AB、AC于E、F,若BE+CF=7.则EF=( )