题目内容

5．如图，一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A，B两点，使不等式ax+b＞$\frac{k}{x}$成立的自变量x的取值范围是（　　）
A．x＜-1或x＞4B．x＜-1或0＜x＜4C．-1＜x＜4D．-1＜x＜0或x＞4

分析 根据两函数图象的上下位置关系结合交点横坐标即可找出不等式的解集，此题得解．

解答 解：观察函数图象可发现：当x＜-1或0＜x＜4时，一次函数图象在反比例函数图象上方，
∴使不等式ax+b＞$\frac{k}{x}$成立的自变量x的取值范围是x＜-1或0＜x＜4．
故选B．

点评 本题考查了反比例函数与一次函数的交点问题，根据两函数图象的上下位置关系结合交点的横坐标找出不等式的解集是解题的关键．

练习册系列答案
相关题目
15．数学问题：如图1，在△ABC中，∠A=α，∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1，求∠BOn-1C的度数？

问题探究：我们从较为简单的情形入手．
探究一：如图2，在△ABC中，∠A=α，∠ABC、∠ACB的角平分线分别交于点O1，求∠BO1C的度数？
解：由题意可得∠O1BC=$\frac{1}{2}$∠ABC，∠O1CB=$\frac{1}{2}$∠ACB
∴∠O1BC+∠O1CB=$\frac{1}{2}$（∠ABC+∠ACB）=$\frac{1}{2}$（180°-α）
∴∠BO1C=180°-$\frac{1}{2}$（180°-α）=90°+$\frac{1}{2}$α．
探究二：如图3，∠A=α，∠ABC、∠ACB三等分线分别交于点O1、O2，求∠BO2C的度数．
解：由题意可得∠O2BC=$\frac{2}{3}$∠ABC，∠O2CB=$\frac{2}{3}$∠ACB
∴∠O2BC+∠O2CB=$\frac{2}{3}$（∠ABC+∠ACB）=$\frac{2}{3}$（180°-α）
∴∠BO2C=180°-$\frac{2}{3}$（180°-α）=60°+$\frac{2}{3}$α．
探究三：如图4，∠A=α，∠ABC、∠ACB四等分线分别交于点O1、O2、O3，求∠BO3C的度数．
（仿照上述方法，写出探究过程）
问题解决：如图1，在△ABC中，∠A=α，∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1，求∠BOn-1C的度数．
问题拓广：
如图2，在△ABC中，∠A=α，∠ABC、∠ACB的角平分线交于点O1，两条角平分线构成一角∠BO1C．
得到∠BO1C=90°+$\frac{1}{2}$α．
探究四：如图3，∠A=α，∠ABC、∠ACB三等分线分别交于点O1、O2，四条等分线构成两个角∠BO1C，∠BO2C，则∠BO2C+∠BO1C=180°+α．
探究五：如图4，∠A=α，∠ABC、∠ACB四等分线分别交于点O1、O2、O3，六等分线构成两个角∠BO3C，∠BO2C，∠BO1C，则∠BO3C+∠BO2C+∠BO1C=270°+$\frac{3}{2}$α．
探究六：如图1，在△ABC中，∠A=α，∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1，（2n-2））等分线构成（n-1）个角∠BOn-1C…∠BO3C，∠BO2C，∠BO1C，则∠BOn-1C+…∠BO3C+∠BO2C+∠BO1C=（n-1）（90°+$\frac{1}{2}$α）．
16．用适当的方法解下列方程
（Ⅰ）x2-1=4（x+1）
（Ⅱ）3x2-6x+2=0．
13．如图，点A为函数y=$\frac{9}{x}$（x＞0）的图象上一点，连接OA，交函数y=$\frac{1}{x}$（x＞0）的图象于点B，点C是x轴上一点，且AO=AC，则△ABC的面积是（　　）
A．$\frac{9}{2}$B．9C．6D．3
20．下列图形中，是三棱柱的展开图的是（　　）
A．B．C．D．
10．下列分解因式正确的是（　　）
A．x3-x=x（x2-1）B．（m+3）（m-2）=m2+m-6C．（a+4）（a-4）=a2-16D．x2-y2=（x-y）（x+y）
17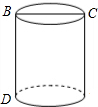．如图，一个圆柱体的底面周长为24，高BD=5，BC是直径．一只蚂蚁从点D出发，沿着表面爬到C的最短路程大约为（　　）
A．13cmB．12cmC．6cmD．16cm
14．如图，二次函数y=ax2+bx+c的图象开口向上，对称轴为直线x=1，图象经过（3，0），下列结论中，正确的一项是（　　）
A．abc＜0B．4ac-b2＜0C．a-b+c＜0D．2a+b＜0
15．下列关于函数y=$\frac{1}{2}$（x-6）2+3的图象，下列叙述错误的是（　　）
A．图象是抛物线，开口向上
B．对称轴为直线x=6
C．顶点是图象的最高点，坐标为（6，3）
D．当x＜6时，y随x的增大而减小；当x＞6时，y随x的增大而增大

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网