题目内容
17.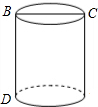 如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程大约为( )
如图,一个圆柱体的底面周长为24,高BD=5,BC是直径.一只蚂蚁从点D出发,沿着表面爬到C的最短路程大约为( )| A. | 13cm | B. | 12cm | C. | 6cm | D. | 16cm |
分析 根据题意,先将圆柱体展开,再根据两点之间线段最短.
解答 解:将圆柱体展开,连接DC,
圆柱体的底面周长为24,则DE=12,
根据两点之间线段最短,
CD=$\sqrt{{5}^{2}+1{2}^{2}}$=13.
而走B-D-C的距离更短,
∵BD=5,BC=$\frac{24}{π}$,
∴BD+BC≈12.
故选:B.
点评 本题考查了平面展开--最短路径问题,将圆柱体展开,根据两点之间线段最短,运用勾股定理解答即可.

练习册系列答案
相关题目
5. 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | x<-1或0<x<4 | C. | -1<x<4 | D. | -1<x<0或x>4 |
12.抛物线 y=-(x-1)2-2 的顶点坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (-1,2) | D. | (1,-2) |
2. 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )| A. | 4 | B. | 8 | C. | 10 | D. | 6 |
9. 如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
 如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )| A. | 3.2m | B. | 4m | C. | 3.5m | D. | 4.2m |
6. 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.下列语句中,是命题的是( )
| A. | 有公共顶点的两个角是对顶角 | B. | 在一条直线上任取一点A | ||
| C. | 过点A作直线MN的垂线 | D. | 过点A作直线MN的平行线 |
 (1)观察思考
(1)观察思考