题目内容
15.数学问题:如图1,在△ABC中,∠A=α,∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1,求∠BOn-1C的度数?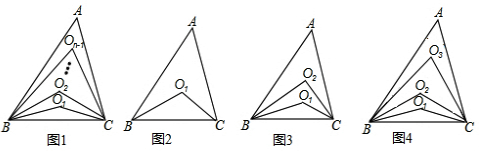
问题探究:我们从较为简单的情形入手.
探究一:如图2,在△ABC中,∠A=α,∠ABC、∠ACB的角平分线分别交于点O1,求∠BO1C的度数?
解:由题意可得∠O1BC=$\frac{1}{2}$∠ABC,∠O1CB=$\frac{1}{2}$∠ACB
∴∠O1BC+∠O1CB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-α)
∴∠BO1C=180°-$\frac{1}{2}$(180°-α)=90°+$\frac{1}{2}$α.
探究二:如图3,∠A=α,∠ABC、∠ACB三等分线分别交于点O1、O2,求∠BO2C的度数.
解:由题意可得∠O2BC=$\frac{2}{3}$∠ABC,∠O2CB=$\frac{2}{3}$∠ACB
∴∠O2BC+∠O2CB=$\frac{2}{3}$(∠ABC+∠ACB)=$\frac{2}{3}$(180°-α)
∴∠BO2C=180°-$\frac{2}{3}$(180°-α)=60°+$\frac{2}{3}$α.
探究三:如图4,∠A=α,∠ABC、∠ACB四等分线分别交于点O1、O2、O3,求∠BO3C的度数.
(仿照上述方法,写出探究过程)
问题解决:如图1,在△ABC中,∠A=α,∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1,求∠BOn-1C的度数.
问题拓广:
如图2,在△ABC中,∠A=α,∠ABC、∠ACB的角平分线交于点O1,两条角平分线构成一角∠BO1C.
得到∠BO1C=90°+$\frac{1}{2}$α.
探究四:如图3,∠A=α,∠ABC、∠ACB三等分线分别交于点O1、O2,四条等分线构成两个角∠BO1C,∠BO2C,则∠BO2C+∠BO1C=180°+α.
探究五:如图4,∠A=α,∠ABC、∠ACB四等分线分别交于点O1、O2、O3,六等分线构成两个角∠BO3C,∠BO2C,∠BO1C,则∠BO3C+∠BO2C+∠BO1C=270°+$\frac{3}{2}$α.
探究六:如图1,在△ABC中,∠A=α,∠ABC、∠ACB的n等分线分别交于点O1、O2、…、On-1,(2n-2))等分线构成(n-1)个角∠BOn-1C…∠BO3C,∠BO2C,∠BO1C,则∠BOn-1C+…∠BO3C+∠BO2C+∠BO1C=(n-1)(90°+$\frac{1}{2}$α).
分析 探究三:借助探究一,二找出规律,即可得出结论;
问题解决:借助探究一,二,三找出规律即可得出结论;
探究四:借助问题解决的方法即可得出结论;
探究五:同探究四的方法即可;
探究六:同探究四的方法即可.
解答 解:探究三:由题意可得∠O3BC=$\frac{3}{4}$∠ABC,∠O3CB=$\frac{3}{4}$∠ACB
∴∠O3BC+∠O3CB=$\frac{3}{4}$(∠ABC+∠ACB)=$\frac{3}{4}$(180°-α)
∴∠BO3C=180°-$\frac{3}{4}$(180°-α)=$\frac{90°}{2}$+$\frac{3}{4}$α.
问题解决:由题意可得∠On-1BC=$\frac{n-1}{n}$∠ABC,∠On-1CB=$\frac{n-1}{n}$∠ACB
∴∠On-1BC+∠On-1CB=$\frac{n-1}{n}$(∠ABC+∠ACB)=$\frac{n-1}{n}$(180°-α)
∴∠BOn-1C=180°-$\frac{n-1}{n}$(180°-α)=$\frac{180°}{n}$+$\frac{n-1}{n}$α.
探究四:由题意可得∠O1BC=$\frac{1}{3}$∠ABC,∠O1CB=$\frac{1}{3}$∠ACB
∴∠O1BC+∠O1CB=$\frac{1}{3}$(∠ABC+∠ACB)=$\frac{1}{3}$(180°-α)
∴∠BO1C=180°-$\frac{1}{3}$(180°-α)=120°+$\frac{1}{3}$α.
由探究二得,∠BO2C=60°+$\frac{2}{3}$α.
∴∠BO2C+∠BO1C=60°+$\frac{2}{3}$α+120°+$\frac{1}{3}$α=180°+α.
故答案为:180°+α;
探究五:由题意可得∠O1BC=$\frac{1}{4}$∠ABC,∠O1CB=$\frac{1}{4}$∠ACB
∴∠O1BC+∠O1CB=$\frac{1}{4}$(∠ABC+∠ACB)=$\frac{1}{4}$(180°-α)
∴∠BO1C=180°-$\frac{1}{4}$(180°-α)=135°+$\frac{1}{4}$α.
由题意可得∠O2BC=$\frac{1}{2}$∠ABC,∠O2CB=$\frac{1}{2}$∠ACB
∴∠O2BC+∠O2CB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-α)
∴∠BO2C=180°-$\frac{1}{2}$(180°-α)=90°+$\frac{1}{2}$α.
由题意可得∠O3BC=$\frac{3}{4}$∠ABC,∠O3CB=$\frac{3}{4}$∠ACB
∴∠O3BC+∠O3CB=$\frac{3}{4}$(∠ABC+∠ACB)=$\frac{3}{4}$(180°-α)
∴∠BO3C=180°-$\frac{3}{4}$(180°-α)=45°+$\frac{3}{4}$α.
∴∠BO3C+∠BO2C+∠BO1C=45°+$\frac{3}{4}$α+90°+$\frac{1}{2}$α+135°+$\frac{1}{4}$α=270°+$\frac{3}{2}$α.
故答案为270°+$\frac{3}{2}$α.
探究六:由题意可得∠O1BC=$\frac{1}{n}$∠ABC,∠O1CB=$\frac{1}{n}$∠ACB
∴∠O1BC+∠O1CB=$\frac{1}{n}$(∠ABC+∠ACB)=$\frac{1}{n}$(180°-α)
∴∠BO1C=180°-$\frac{1}{n}$(180°-α)=$\frac{n-1}{n}$•180°+$\frac{1}{n}$α.
由题意可得∠O2BC=$\frac{2}{n}$∠ABC,∠O2CB=$\frac{2}{n}$∠ACB
∴∠O2BC+∠O2CB=$\frac{2}{n}$(∠ABC+∠ACB)=$\frac{2}{n}$(180°-α)
∴∠BO2C=180°-$\frac{2}{n}$(180°-α)=$\frac{n-2}{n}$•180°+$\frac{2}{n}$α.
由题意可得∠O3BC=$\frac{3}{n}$∠ABC,∠O3CB=$\frac{3}{n}$∠ACB
∴∠O3BC+∠O3CB=$\frac{3}{n}$(∠ABC+∠ACB)=$\frac{3}{n}$(180°-α)
∴∠BO3C=180°-$\frac{3}{n}$(180°-α)=$\frac{n-3}{n}$•180°+$\frac{3}{n}$α.
…
由问题解决得,∠BOn-1C=$\frac{180°}{n}$+$\frac{n-1}{n}$α.
∴∠BOn-1C+…∠BO3C+∠BO2C+∠BO1C
=$\frac{180°}{n}$+$\frac{n-1}{n}$α+…+$\frac{n-3}{n}$•180°+$\frac{3}{n}$α+$\frac{n-2}{n}$•180°+$\frac{2}{n}$α+$\frac{n-1}{n}$•180°+$\frac{1}{n}$α
=($\frac{1}{n}$+$\frac{2}{n}$+…$\frac{n-3}{n}$+$\frac{n-2}{n}$+$\frac{n-1}{n}$)•180°+($\frac{n-1}{n}$+$\frac{n-2}{n}$+…+$\frac{3}{n}$+$\frac{2}{n}$+$\frac{1}{n}$)•α
=($\frac{1}{n}$+$\frac{2}{n}$+…$\frac{n-3}{n}$+$\frac{n-2}{n}$+$\frac{n-1}{n}$)•(180°+α)
=$\frac{1}{2}$(n-1)•(180°+α)
=(n-1)(90°+$\frac{1}{2}$α).
故答案为:(n-1)(90°+$\frac{1}{2}$α).
点评 此题以三角形的内角和为背景,考查了角等分线,前(n-1)个正整数的和的计算方法,提取公因式,体现了类比的思想,解本题的关键是找出规律,解此类题目的方法时,从简单到复杂的过程中,寻找规律.

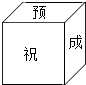 妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )
妈妈为今年参加中考的女儿小红制作了一个正方体礼品盒(如图),六个面上各有一个字,连起来就是“预祝中考成功”,其中“祝”的对面是“考”,“成”的对面是“功”,则它的平面展开图可能是( )| A. |  | B. | 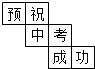 | C. | 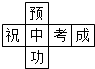 | D. |  |
| A. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{{x}^{2}-9}{{x}^{2}+6x+9}$=$\frac{x-3}{x+3}$ | D. | $\frac{0.2a+b}{a+0.5b}$=$\frac{2a+b}{a+5b}$ |
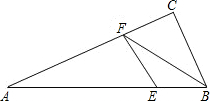 如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,E为AB上一点,且AE:EB=4:1,EF⊥AC于F,连结FB,则tan∠CFB的值等于( )| A. | $\frac{5\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 5$\sqrt{3}$ |
 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | x<-1或0<x<4 | C. | -1<x<4 | D. | -1<x<0或x>4 |
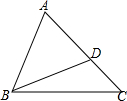 如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,AC=9.
如图,D是△ABC的边AC上的一点,连接BD,已知∠ABD=∠C,AB=6,AD=4,AC=9.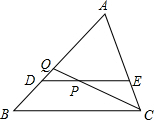 如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.
如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.