题目内容
14. 如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )| A. | abc<0 | B. | 4ac-b2<0 | C. | a-b+c<0 | D. | 2a+b<0 |
分析 根据二次函数图象开口向上,判断a大于0,与y轴交于负半轴,判断c小于0,对称轴为直线x=1,判断b<0,据此对选项A作出判断;根据对称轴为直线x=1,即可对选项D作出判断;根据二次函数对称轴为直线x=1,图象经过(3,0),进而得到二次函数图象与x轴另一个交点为(-1,0),坐标代入解析式,即可对选项C作出判断;根据二次函数图象与x轴有两个交点,即可对选项B作出判断.
解答 解:∵二次函数图象开口向上,
∴a>0,
∵二次函数图象与y轴交于负半轴,
∴c<0,
∵二次函数图象的对称轴是直线x=1,
∴-$\frac{b}{2a}$=1,
∴b<0,2a+b=0,
∴abc>0,
∴A,B选项错误,
∵二次函数图象经过(3,0),对称轴为x=1,
∴二次函数图象与x轴另一个交点为(-1,0),
∴a-b+c=0,故此选项C错误;
∵二次函数与x轴有两个交点,
∴b2-4ac>0,则4ac-b2<0,故选项B正确,
故选:B.
点评 此题主要考查了抛物线与x轴交点性质,得出图象与x轴的另一个坐标是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | x<-1或0<x<4 | C. | -1<x<4 | D. | -1<x<0或x>4 |
2. 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )| A. | 4 | B. | 8 | C. | 10 | D. | 6 |
9. 如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
 如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )
如图,AB是斜靠在墙上的长梯,梯脚B距墙角1.4m,楼上点D距离墙1.2m,BD长0.5m,则梯子的长为( )| A. | 3.2m | B. | 4m | C. | 3.5m | D. | 4.2m |
19. 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
 若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )
若a、b两数在数轴上的位置如图所示,则下列结论正确的是( )| A. | a+b>0 | B. | a-b<0 | C. | ab>0 | D. | $\frac{a}{b}$>0 |
6. 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3. 如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
 如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )
如图,小明从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了( )| A. | 240m | B. | 230m | C. | 220m | D. | 200m |
4.下列运算中,正确的是( )
| A. | x3•x3=x6 | B. | 3x2+2x3=5x5 | C. | (x2)3=x5 | D. | (ab)3=a3b |
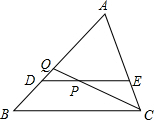 如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.
如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.