题目内容
16.用适当的方法解下列方程(Ⅰ)x2-1=4(x+1)
(Ⅱ)3x2-6x+2=0.
分析 (I)整理后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(II)先求出b2-4ac的值,再代入公式求出即可.
解答 解:(I)移项得:(x+1)(x-1)-4(x+1)=0,
(x+1)(x-1-4)=0,
x+1=0,x-5=0,
x1=-1,x2=5;
(II)3x2-6x+2=0,
b2-4ac=(-6)2-4×3×2=12,
x=$\frac{6±\sqrt{12}}{2×3}$,
x1=$\frac{3+\sqrt{3}}{3}$,x2=$\frac{3-\sqrt{3}}{3}$.
点评 本题考查了解一元二次方程,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.下列从左到右的变形,错误的是( )
| A. | $\frac{a}{b}$=$\frac{ac}{bc}$(c≠0) | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{{x}^{2}-9}{{x}^{2}+6x+9}$=$\frac{x-3}{x+3}$ | D. | $\frac{0.2a+b}{a+0.5b}$=$\frac{2a+b}{a+5b}$ |
1. 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )
 如图所示的几何体从上面看得到的平面图形是( )
如图所示的几何体从上面看得到的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
5. 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
 如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )
如图,一次函数y=ax+b和反比例函数y=$\frac{k}{x}$的图象相交于A,B两点,使不等式ax+b>$\frac{k}{x}$成立的自变量x的取值范围是( )| A. | x<-1或x>4 | B. | x<-1或0<x<4 | C. | -1<x<4 | D. | -1<x<0或x>4 |
6. 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
 如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )
如图,在4×5的正方形网格中,已有线段AB,在格点中再取一点C,使△ABC成为等腰三角形,这样的点C有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
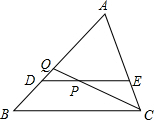 如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15.
如图,DE∥BC,且过△ABC的重心,分别与AB、AC交于点D、E,点P是线段DE上一点,CP的延长线交AB于点Q,如果$\frac{DP}{DE}$=$\frac{1}{4}$,那么S△DPQ:S△CPE的值是1:15. 观察思考:
观察思考: (1)观察思考
(1)观察思考