题目内容
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论:
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,现有以下结论:①a+b+c=0;②b>2a;③ax2+bx+c=0的两根分别为-3和1;④a-2b+c>0.
其中正确的结论是
考点:二次函数图象与系数的关系
专题:
分析:根据抛物线与x轴的交点坐标为(1,0)对①进行判断;
根据对称轴方程为x=-
=-1对②进行判断;
根据抛物线的对称性得到抛物线与x轴的交点坐标为(-3,0)和(1,0),由此对③进行判断;
根据抛物线与y轴的交点在x轴下方,得到c<0,而a+b+c=0,则a-2b+c=-3b,由b>0,于是可对④进行判断.
根据对称轴方程为x=-
| b |
| 2a |
根据抛物线的对称性得到抛物线与x轴的交点坐标为(-3,0)和(1,0),由此对③进行判断;
根据抛物线与y轴的交点在x轴下方,得到c<0,而a+b+c=0,则a-2b+c=-3b,由b>0,于是可对④进行判断.
解答:解:∵x=1时,y=0,
∴a+b+c=0,所以①正确;
∵x=-
=-1,
∴b=2a,所以②错误;
∵点(1,0)关于直线x=-1对称的点的坐标为(-3,0),
∴抛物线与x轴的交点坐标为(-3,0)和(1,0),
∴ax2+bx+c=0的两根分别为-3和1,所以③正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
而a+b+c=0,b=2a,
∴c=-3a,
∴a-2b+c=-3b,
∵b>0,
∴-3b<0,所以④错误.
故答案为①③.
∴a+b+c=0,所以①正确;
∵x=-
| b |
| 2a |
∴b=2a,所以②错误;
∵点(1,0)关于直线x=-1对称的点的坐标为(-3,0),
∴抛物线与x轴的交点坐标为(-3,0)和(1,0),
∴ax2+bx+c=0的两根分别为-3和1,所以③正确;
∵抛物线与y轴的交点在x轴下方,
∴c<0,
而a+b+c=0,b=2a,
∴c=-3a,
∴a-2b+c=-3b,
∵b>0,
∴-3b<0,所以④错误.
故答案为①③.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-
;抛物线与y轴的交点坐标为(0,c).
| b |
| 2a |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一只蚂蚁从数轴上A点出发爬了4个单位长度到了表示-1的点B,则点A所表示的数是( )
| A、-3或5 | B、-5或3 |
| C、-5 | D、3 |
下列说法错误的是( )
| A、三个外角(每个顶点处各取一个外角)都相等的三角形是等边三角形 |
| B、有一个角为60°的等腰三角形是等边三角形 |
| C、有两角相等的等腰三角形是等边三角形 |
| D、一腰上的中线也是这条腰上的高的等腰三角形是等边三角形 |
 如图,判断两个三角形是否相似,并求出x和y.
如图,判断两个三角形是否相似,并求出x和y.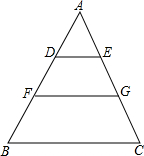 如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC.
如图,△ABC中,D、F在AB上,且AD=BF,DE∥BC交AC于E,FG∥BC交AC于G.求证:DE+FG=BC. 如图,已知:在△ABC中,D、E是BC上的两点,且AD=BD,AE=CE,∠ADE=82°,∠AED=48°,则∠BAC=
如图,已知:在△ABC中,D、E是BC上的两点,且AD=BD,AE=CE,∠ADE=82°,∠AED=48°,则∠BAC=