题目内容
15．
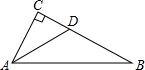如图，在△ABC中，∠C=90°，∠CAB的角平分线AD交BC于点D，若BC=20，BD：CD=3：2，则点D到AB的距离为（ ）| A． | 8 | B． | 12 | C． | 4 | D． | 20 |
分析 作DE⊥AB于E，根据题意求出CD的长，根据角平分线的性质得到DE=CD，得到答案．
解答 
解：作DE⊥AB于E，
∵BC=20，BD：CD=3：2，
∴CD=8，
∵AD是∠CAB的角平分线，∠C=90°，DE⊥AB，
∴DE=CD=8，
故选：A．
点评 本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
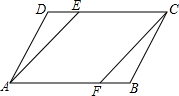如图，在平行四边形ABCD中，BF=DE，求证：∠BAE=∠DCF．
小明和小华在一栋大楼的前面估计楼房高度．小明说这楼有20层！小华说没有20层．为了验证他们的观点，他们在大楼两侧选择A、B两个点，经过测量AB=150米，CD=10米．∠A=30°，∠B=45°．不计两个人的身高，且A、B、C、D四个点在同一直线上．
如图，从A路口到B路口有①、②、③三条路线可走，人们一般情况下选择走②号路线，用几何知识解释其道理应是两点之间，线段最短．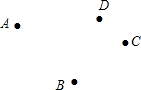
已知平面上A、B、C、D四个点，请用直尺按下列步骤要求完成画图．
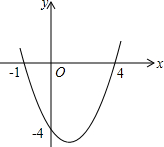二次函数y=ax2+bx+c的图象如图所示，求：