题目内容
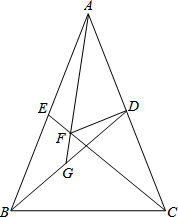 已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G.
已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G.(1)求证:AD2=DG•BD;
(2)联结CG,求证:∠ECB=∠DCG.
考点:相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质
专题:证明题
分析:(1)根据已知求出AD=AE,根据SAS证出△BAD≌△CAE,得出∠ABD=∠ACE,再根据DF⊥AC,AD=CD,得出AF=CF,∠GAD=∠ACE,从而得出∠GAD=∠ABD,再根据AA证出△GDA∽△ADB,得出
=
,即可得出AD2=DG•BD;
(2)在(1)的基础上证明△DCG∽△DBC,根据相似三角形的性质可以得到相应的答案.
| AD |
| DB |
| DG |
| AD |
(2)在(1)的基础上证明△DCG∽△DBC,根据相似三角形的性质可以得到相应的答案.
解答:证明:(1)∵AB=AC,AD=
AC,AE=
AB,
∴AD=AE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE.
∴∠ABD=∠ACE,
∵DF⊥AC,AD=CD,
∴AF=CF,
∴∠GAD=∠ACE,
∴∠GAD=∠ABD.
∵∠GDA=∠ADB,
∴△GDA∽△ADB.
∴
=
,
∴AD2=DG•BD.
(2)证明:
∵
=
,AD=CD,
∴
=
.
∵∠CDG=∠BDC,
∴△DCG∽△DBC.
∴∠DBC=∠DCG.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACE,
∴∠ECB=∠DBC=∠DCG,
∴∠ECB=∠DCG.
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=AE,
在△BAD和△CAE中,
|
∴△BAD≌△CAE.
∴∠ABD=∠ACE,
∵DF⊥AC,AD=CD,
∴AF=CF,
∴∠GAD=∠ACE,
∴∠GAD=∠ABD.
∵∠GDA=∠ADB,
∴△GDA∽△ADB.
∴
| AD |
| DB |
| DG |
| AD |
∴AD2=DG•BD.
(2)证明:
∵
| AD |
| DB |
| DG |
| AD |
∴
| CD |
| DB |
| DG |
| CD |
∵∠CDG=∠BDC,
∴△DCG∽△DBC.
∴∠DBC=∠DCG.
∵AB=AC,
∴∠ABC=∠ACB.
∵∠ABD=∠ACE,
∴∠ECB=∠DBC=∠DCG,
∴∠ECB=∠DCG.
点评:此题考查了相似形的综合,用到的知识点是相似三角形和全等三角形的判定与性质、等腰三角形的性质,解题的关键是找出相似三角形,利用相似三角形的性质求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知BD是等腰△ABC的角平分线,如果∠A=80°,那么∠ADB等于( )
| A、90° |
| B、75° |
| C、60° |
| D、90°或75°或60° |
下列计算正确的是( )
| A、(x+y)2=x2+y2 |
| B、(x-y)2=x2-2xy-y2 |
| C、(-x+y)2=x2-2xy+y2 |
| D、(x+2y)(x-2y)=x2-2y2 |
 如图,O为原点,线段OA与x轴正半轴重合,且OA=4a,四边形OABC为正方形,以OA为直径作⊙P,过C作⊙P的切线,切点为Q,延长CQ交AB于D.
如图,O为原点,线段OA与x轴正半轴重合,且OA=4a,四边形OABC为正方形,以OA为直径作⊙P,过C作⊙P的切线,切点为Q,延长CQ交AB于D.
