题目内容
 如图,O为原点,线段OA与x轴正半轴重合,且OA=4a,四边形OABC为正方形,以OA为直径作⊙P,过C作⊙P的切线,切点为Q,延长CQ交AB于D.
如图,O为原点,线段OA与x轴正半轴重合,且OA=4a,四边形OABC为正方形,以OA为直径作⊙P,过C作⊙P的切线,切点为Q,延长CQ交AB于D.(1)求证:PQ2=CQ•QD;
(2)若a=1,求过O、Q、A三点的抛物线解析式.
考点:切线的性质,待定系数法求二次函数解析式,相似三角形的判定与性质
专题:计算题
分析:(1)连接CP,DP,根据CD,OC都与圆相切,得到一对直角相等,利用HL得到直角三角形PCO与直角三角形PCQ全等,利用全等三角形对应角相等得到∠CPO=∠CPQ,同理得到∠DPA=∠DPQ,利用平角的定义及等式性质得到∠CPD=90°,利用同角的余角相等得到一对角相等,再由一对直角相等得到三角形CPQ与三角形PQD相似,由相似得比例即可得证;
(2)将a=1代入确定出正方形的边长,进而确定出A坐标,过Q作QN垂直于x轴,连接OQ,根据CO=QO,OP=QP,得到CP垂直平分OQ,即M为OQ中点,利用同角的余角相等得到∠OCP=∠QON,由OP=2,OC=4,求出tan∠OCP的值,即为tan∠QON的值,在直角三角形OCP中,利用面积法求出OM的长,确定出OQ的长,利用锐角三角函数定义求出QN与ON的长,确定出Q坐标,根据A与O坐标设出抛物线的二根式方程,将Q坐标代入即可确定出解析式.
(2)将a=1代入确定出正方形的边长,进而确定出A坐标,过Q作QN垂直于x轴,连接OQ,根据CO=QO,OP=QP,得到CP垂直平分OQ,即M为OQ中点,利用同角的余角相等得到∠OCP=∠QON,由OP=2,OC=4,求出tan∠OCP的值,即为tan∠QON的值,在直角三角形OCP中,利用面积法求出OM的长,确定出OQ的长,利用锐角三角函数定义求出QN与ON的长,确定出Q坐标,根据A与O坐标设出抛物线的二根式方程,将Q坐标代入即可确定出解析式.
解答: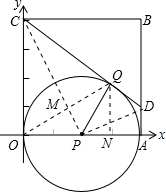 (1)证明:连接CP,DP,
(1)证明:连接CP,DP,
∵AD,CO都与圆O相切,
∴PQ⊥CQ,CO⊥PO,
∴CO=CQ,
在Rt△CPO与Rt△CPQ中,
,
∴Rt△CPO≌Rt△CPQ(HL),
∴∠CPO=∠CPQ,
同理∠DPQ=∠DPQ,
∵∠QPO+∠QPA=180°,即∠CPO+∠CPQ+∠DPQ+∠DPA=180°,
∴∠CPQ+∠QPD=90°,
∵∠CPQ+∠PCQ=90°,
∴∠QPD=∠PCQ,
∵∠PQD=∠CQP=90°,
∴△PDQ∽△CPQ,
∴
=
,即PQ2=CQ•QD;
(2)解:∵a=1,∴A(4,0),
连接OQ,与CP交于点M,过Q作QN⊥x轴,
∵CO=CQ,PO=PQ,
∴CP垂直平分OQ,
∴OM=QM,
∵
CP•OM=
OC•OP,
∴OM=
=
=
,
∴OQ=
,
∵∠OCP=∠QON,
∴tan∠OCP=tan∠QON=
=
,
设QN=x,则有ON=2x,
根据勾股定理得:x2+(2x)2=(
)2,
解得:x=
(负值舍去),
∴Q(
,
),
设抛物线解析式为y=a(x-0)(x-4),
将x=
,y=
代入得:a=-
,
则抛物线解析式为y=-
x2+
x.
 (1)证明:连接CP,DP,
(1)证明:连接CP,DP,∵AD,CO都与圆O相切,
∴PQ⊥CQ,CO⊥PO,
∴CO=CQ,
在Rt△CPO与Rt△CPQ中,
|
∴Rt△CPO≌Rt△CPQ(HL),
∴∠CPO=∠CPQ,
同理∠DPQ=∠DPQ,
∵∠QPO+∠QPA=180°,即∠CPO+∠CPQ+∠DPQ+∠DPA=180°,
∴∠CPQ+∠QPD=90°,
∵∠CPQ+∠PCQ=90°,
∴∠QPD=∠PCQ,
∵∠PQD=∠CQP=90°,
∴△PDQ∽△CPQ,
∴
| PQ |
| CQ |
| QD |
| PQ |
(2)解:∵a=1,∴A(4,0),
连接OQ,与CP交于点M,过Q作QN⊥x轴,
∵CO=CQ,PO=PQ,
∴CP垂直平分OQ,
∴OM=QM,
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴OM=
| OC•OP |
| CP |
| 4×2 | ||
2
|
4
| ||
| 5 |
∴OQ=
8
| ||
| 5 |
∵∠OCP=∠QON,
∴tan∠OCP=tan∠QON=
| OP |
| OC |
| 1 |
| 2 |
设QN=x,则有ON=2x,
根据勾股定理得:x2+(2x)2=(
8
| ||
| 5 |
解得:x=
| 8 |
| 5 |
∴Q(
| 8 |
| 5 |
| 16 |
| 5 |
设抛物线解析式为y=a(x-0)(x-4),
将x=
| 8 |
| 5 |
| 16 |
| 5 |
| 5 |
| 6 |
则抛物线解析式为y=-
| 5 |
| 6 |
| 10 |
| 3 |
点评:此题考查了切线的性质,全等三角形的判定与性质,勾股定理,锐角三角函数定义,熟练掌握切线的性质是解本题的关键.

练习册系列答案
相关题目
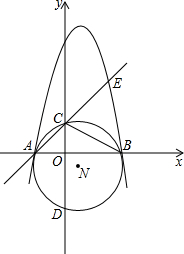 如图:抛物线y=x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于E,且E的横坐标为3,△ABC的外接圆⊙N交y轴于另一点D.
如图:抛物线y=x2+bx+c交x轴于A、B,直线y=x+2过点A,交y轴于C,交抛物线于E,且E的横坐标为3,△ABC的外接圆⊙N交y轴于另一点D.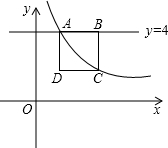 如图,直线y=4和反比例函数y=
如图,直线y=4和反比例函数y=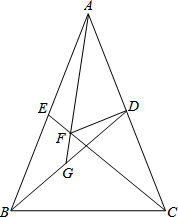 已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G.
已知:如图,在△ABC中,AB=AC,点D、E分别是边AC、AB的中点,DF⊥AC,DF与CE相交于点F,AF的延长线与BD相交于点G.