题目内容
4.求下列各式中x的值(1)(3x+2)2=64
(2)(2x-1)3=-8
(3)9(2x-1)2-25=56
(4)2(x-1)3=$\frac{125}{4}$.
分析 (1)直接开平方得3x+2=8或3x+2=-8,解一元一次方程可得;
(2)直接开立方得2x-1=-2,解该一元一次方程可得;
(3)由9(2x-1)2-25=56得(2x-1)2=9,再开平方后解一元一次方程即可;
(4)由2(x-1)3=$\frac{125}{4}$得(x-1)3=$\frac{125}{8}$,再开立方后解方程即可.
解答 解:(1)∵(3x+2)2=64,
∴3x+2=8或3x+2=-8,
解得:x=2或x=-$\frac{10}{3}$;
(2)∵(2x-1)3=-8,
∴2x-1=-2,
解得:x=-$\frac{1}{2}$;
(3)由9(2x-1)2-25=56得:(2x-1)2=9,
∴2x-1=3或2x-1=-3,
解得:x=2或x=-1;
(4)由2(x-1)3=$\frac{125}{4}$得:(x-1)3=$\frac{125}{8}$,
∴x-1=$\frac{5}{2}$,
解得:x=$\frac{7}{2}$.
点评 本题考查了平方根和立方根的概念.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.立方根的性质:一个正数的立方根式正数,一个负数的立方根是负数,0的立方根式0.

练习册系列答案
相关题目
13.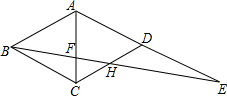 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
 如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )
如图,四边形ABCD是菱形,其边长AB=5,点E为AD的延长线上一点,连接BE,分别交AC、DC于点F、H,BF=DE,FH=2,则DE的长为( )| A. | 2 | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{13}{3}$ |
 如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数.
如图,AB是⊙O的直径,∠D=20°.求∠BAC的度数. 如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.
如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.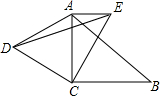 如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.
如图,在△ABC中,∠ACB=90°BC=2,将△ACB绕点C逆时针旋转60°得到△DCE(A和D,B和E分别是对应顶点),若AE∥BC,则△ADE的周长为1+$\sqrt{3}+$$\sqrt{7}$.