题目内容
20．
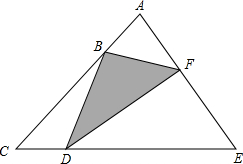已知S△BDF=19cm2，AB：AC=1：4；AF：AE=1：3；CD：CE=1：5，求△ACE的大小．
分析 根据题意，连接AD，BE，CF，根据等高的三角形面积与底的正比关系，即可知道△ABF，△BDC，△EFD与△ACE的关系，进一步得到△BDF与△ACE的关系，即可求得△ACE的面积．
解答 
解：连接AD，BE，CF，
∵AB：AC=1：4；AF：AE=1：3；CD：CE=1：5，S△BDF=19cm2，
∴S△ABF=$\frac{1}{4}$S△ACF=$\frac{1}{4}$×$\frac{1}{3}$S△ACE=$\frac{1}{12}$S△ACE，
S△BCD=$\frac{1}{5}$S△BCE=$\frac{1}{5}$×$\frac{3}{4}$S△ACE=$\frac{3}{20}$S△ACE，
S△DEF=$\frac{4}{5}$S△CEF=$\frac{4}{5}$×$\frac{2}{3}$S△ACE=$\frac{8}{15}$S△ACE，
∴S△BDF=S△ACE-（S△ABF+S△BCD+S△DEF）=$\frac{7}{30}$S△ACE，
∴19=$\frac{7}{30}$S△ACE，
∴S△ACE=$\frac{570}{7}$（cm2）．
点评 本题考查了三角形面积与底的正比关系，关键是熟练高一定时，三角形的面积与底成正比关系的灵活运用．
练习册系列答案
相关题目
如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为20cm2和14cm2，则△EDF的面积为3cm2．
8．
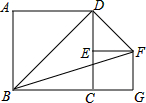如图，菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上，点E在线段CD上，AB=2，∠ABC=60°，则△BDF的面积为（ ）
如图，菱形ABCD与菱形ECGF的顶点B、C、G在同一直线上，点E在线段CD上，AB=2，∠ABC=60°，则△BDF的面积为（ ）| A． | $\frac{\sqrt{3}}{2}$ | B． | $\sqrt{3}$ | C． | $\frac{3\sqrt{3}}{2}$ | D． | 2$\sqrt{3}$ |
如图，在△ABC中，三个内角的角平分线交于点O，OF⊥BC于点E，若∠AOB=130°，求∠COF的度数．
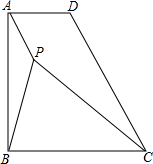已知在直角梯形ABCD中，∠ABC=90°，AB=BC，点P是梯形内一点，且PA=1，PB=2，PC=3
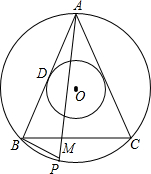如图，已知△ABC内接于以点O为同心圆的大圆⊙O，且AB=AC，腰AB切小圆⊙O于点D．P是$\widehat{BC}$上的动点（不与点B、C重合），AP交BC于点M．