题目内容
1. 如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.(1)若P、Q同时分别从B、C出发,那么几秒后,△PCQ的面积等于4?
(2)若P、Q同时分别从B、C出发,那么几秒后,PQ的长度等于5?
(3)△PCQ的面积何时最大,最大面积是多少?
分析 (1)分别表示出线段CP和线段CQ的长,利用三角形的面积公式列出方程求解即可;
(2)表示出线段CP和CQ后利用勾股定理列出方程求解即可;
(3)列出△PCQ的面积关于t的函数解析式,配方可得最大值.
解答 解:(1)设t秒后△PCQ的面积等于4,根据题意得:CQ=t,BP=2t,则CP=7-2t,
$\frac{1}{2}$CQ•CP=$\frac{1}{2}$×t(7-2t)=4,
整理,得:t1=$\frac{7+\sqrt{17}}{4}$,t2=$\frac{7-\sqrt{17}}{4}$,
故若P、Q同时分别从B、C出发,那么$\frac{7+\sqrt{17}}{4}$、$\frac{7-\sqrt{17}}{4}$秒后,△PCQ的面积等于4;
(2)若PQ的长度等于5,则PC2+QC2=PQ2,
即:(7-2t)2+t2=25,
整理,得:5t2-28t+24=0,
解得:t1=$\frac{14+2\sqrt{19}}{5}$,t2=$\frac{14-2\sqrt{19}}{5}$,
∵CP=7-2t≥0,即t≤3.5,
∴t=$\frac{14+2\sqrt{19}}{5}$>3.5,舍去,
故那么$\frac{14-2\sqrt{19}}{5}$秒后,PQ的长度等于5;
(3)由(1)知△PCQ的面积S=$\frac{1}{2}$×t(7-2t)=-(t-$\frac{7}{4}$)2+$\frac{49}{16}$,
当t=$\frac{7}{4}$时,S取得最大值,最大值为$\frac{49}{16}$,
故当t=$\frac{7}{4}$时△PCQ的面积最大,最大面积为$\frac{49}{16}$.
点评 本题主要考查一元二次方程的应用及二次函数最值的求法,表示出所涉及的线段是前提,根据面积和勾股定理列出方程、函数表达式是关键.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案| A. | ax2+bx+c=0 | B. | x2-2x=x2+1 | C. | 4x2-9=(2x-1)2 | D. | x2-1=0 |
| A. | x2=15×3 | B. | x(x-1)=15×3 | C. | $\frac{1}{2}x({x-1})=15×3$ | D. | $\frac{1}{2}x({x+1})=15×3$ |
| A. | 2014 | B. | -2014 | C. | 1 | D. | -1 |
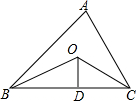 如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )
如图,在△ABC中,BO,CO分别平分∠ABC,OD⊥BC于点D,以点O为圆心,OD长为半径作圆,则AB与⊙O的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 无法确定 |
| A. | 3cm | B. | 4cm | C. | 9cm | D. | 10cm |
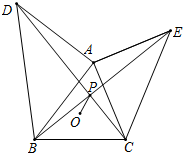 如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$.
如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是3-$\sqrt{3}$. 探究问题.
探究问题. 已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.
已知?ABCD中,点E,F分别是AD,CB延长线上的点,且∠1=∠2,DF交AB于点G,BE交CD于点H,求证:EH=FG.