题目内容
16.学校体育节要组织一次班际乒乓球赛,参赛的每两个班之间都要比赛一场,根据场地和时间等条件,赛程计划安排15天,每天安排3场比赛.设有x个班参加比赛,则x满足的关系式为( )| A. | x2=15×3 | B. | x(x-1)=15×3 | C. | $\frac{1}{2}x({x-1})=15×3$ | D. | $\frac{1}{2}x({x+1})=15×3$ |
分析 关系式为:球队总数×每支球队需赛的场数÷2=3×15,把相关数值代入即可.
解答 解:每支球队都需要与其他球队赛(x-1)场,但2队之间只有1场比赛,
所以可列方程为:$\frac{1}{2}$x(x-1)=3×15.
故选C.
点评 本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到比赛总场数的等量关系,注意2队之间的比赛只有1场,最后的总场数应除以2.

练习册系列答案
相关题目
7.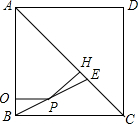
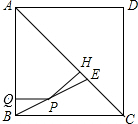 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )

 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
11.一个口袋中有红、白、黑球共10个,这些球除颜色外都相同,将口袋中的球搅拌均匀,从中随机摸出一个球,记下颜色后放回袋中.不断重复这个过程,共摸了100次球,发现有49次摸到红球,21次摸到黑球,则袋中白球大约是( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
8.法国病毒学家团队2014年3月4日宣布,他们发现了世界上第三种超大型病毒,这种巨型史前病毒直径超过0.00000025米,0.0000005用科学记数法可表示为( )
| A. | 5×10-8 | B. | 5×10-9 | C. | 0.5×10-6 | D. | 0.05×10-5 |
5.如今的合肥正在努力实现由国家园林城市向国家生态园林城市的目标跨越,合肥上下掀起“爱绿护绿”热潮,建好后的大蜀山森林公园将真正成为“合肥绿肥”,经过两年时间,绿地面积增加了44%,这两年绿地面积的平均增长率是( )
| A. | 12% | B. | 20% | C. | 21% | D. | 22% |
6.下列命题中错误的是( )
| A. | 平行四边形的对角线互相平分 | |
| B. | 一组对边平行,一组对角相等的四边形是平行四边形 | |
| C. | 等腰梯形的对角线相等 | |
| D. | 两对邻角互补的四边形是平行四边形 |
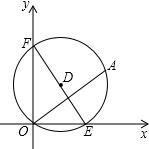 如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$.
如图,在平面直角坐标系中,点A的坐标是(4,3),动圆D经过A、O,分别与两坐标轴的正半轴交于点E、F.当EF⊥OA时,此时EF=$\frac{125}{24}$. 如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.
如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值. 如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.