题目内容
12. 探究问题.
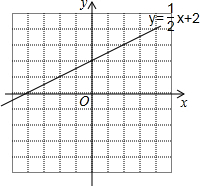
探究问题.(1)实践和操作:如图对于一次函数$\frac{1}{2}$x+2,在直线上取点A(-2,1),B(4,4),将他们向下平移5个单位,得到点A′、B′.
①试写出A′、B′的坐标;
②求出直线A′B′的一次函数表达式,并画出直线A′B′.
(2)观察和归纳:
①从位置关系上观察,你认为直线AB与直线A′B′存在什么关系?
②从直线AB与直线A′B′的表达式观察,你认为两个表达式中相同的是什么?不同的是什么?
③根据你的观察,请归纳出一个一般结论:一次项的系数相同,常数项不同,则两直线平行.(用自己的语言或数字符号描述)
④写出与直线y=-2x+1平行的一条直线是y=-2x-3.
(3)结论验证:
用你所学的知识,说明直线y=-2x+1与你写出的一条直线是平行的道理.
分析 (1)根据平移的性质得出A′、B′的坐标即可,再利用待定系数法得出一次函数关系式;
(2)根据画出的直线和直线的解析式进行解答;
(3)根据两直线的交点的求法进行证明.
解答 解:(1)①∵点A(-2,1),B(4,4),
∴将他们向下平移5个单位,可得:A'(-2,-4),B'(4,-1);
②设直线A'B'的一次函数表达式为;y=kx+b,则有
$\left\{\begin{array}{l}{-2k+b=-4}\\{4k+b=-1}\end{array}\right.$,
解得k=$\frac{1}{2}$,b=-3.
所以A'B'所在直线的表达式为y=$\frac{1}{2}$x-3,
画出直线A'B'如图:
(2)①通过观察可知,直线AB与直线A'B'互相平行,
②通过直线AB与直线A'B'的表达式观察,两个表达式中一次项的系数相同,常数项不同.
③对于直线L1:y=k1x+b1,L2:y=k2x+b2,如果L1∥L2,
则k1=k2,且b1≠b2,反之亦然.
④y=-2x-3,
(3)$\left\{\begin{array}{l}{y=-2x+1}\\{y=-2x-3}\end{array}\right.$,
方程组无解,
故y=-2x+1与y=-2x-3没有交点,则直线y=-2x+1与y=-2x-3平行.
点评 本题考查的是一次函数的有关知识,掌握待定系数法求一次函数解析式、利用方程思想求两直线的交点是解题的关键.

练习册系列答案
相关题目
7.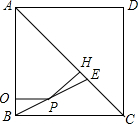
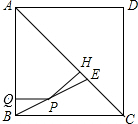 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )

 如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )
如图,正方形ABCD中,AC=2$\sqrt{2}$,对角线AC上点E,且AE=AD,连接BE,P为BE上的动点(与B、E不重合),过P作PQ⊥AB,PH⊥AC分别AB、AC于点Q、H,则PQ+PH的值等于( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
17.若点(-2,y1),(1,y2),(3,y3)都在反比例函数$y=-\frac{6}{x}$的图象上,则y1,y2,y3的大小关系是( )
| A. | y1<y3<y2 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
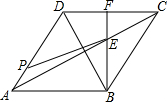 已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.
已知菱形ABCD边长为5cm,tan∠DAB=$\frac{4}{3}$,连接AC、BD,过点B作BE⊥AB分别交AC、CD于E、F.若点P为AD上一点,且∠DPE+∠DAB=90°,则AP长为$\frac{5}{3}$.

 如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值.
如图,⊙O的半径为10cm,G是直径AB上一点,弦CD经过点G,CD=16cm,AE⊥CD于E,BF⊥CD于F,求AE-BF的值. 如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.
如图,△ABC中,∠C=90°,BC=7cm,AC=5,点P从B点出发,沿BC方向以2m/s的速度移动,点Q从C出发,沿CA方向以1m/s的速度移动.