题目内容
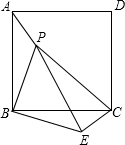 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转与△CBE重合,若PB=3,则PE=考点:旋转的性质
专题:
分析:根据旋转的性质可得∠PBE=∠ABC=90°,PB=PE,然后判断出△PBE是等腰直角三角形,再根据等腰直角三角形的斜边等于直角边的
倍列式计算即可得解.
| 2 |
解答:解:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵△ABP绕点B顺时针方向旋转与△CBE重合,
∴∠PBE=∠ABC=90°,PB=PE,
∴△PBE是等腰直角三角形,
∴PE=
PB=3
.
故答案为:3
.
∴∠ABC=90°,
∵△ABP绕点B顺时针方向旋转与△CBE重合,
∴∠PBE=∠ABC=90°,PB=PE,
∴△PBE是等腰直角三角形,
∴PE=
| 2 |
| 2 |
故答案为:3
| 2 |
点评:本题考查了旋转的性质,等腰直角三角形的判定与性质,正方形的性质,熟记各性质并判断出△PBE是等腰直角三角形是解题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
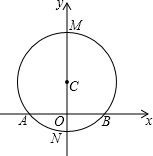 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标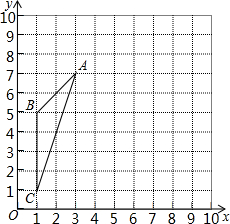 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,



 如图,AB=AD,∠BAD=∠CAE,AC=AE,求证:BC=DE.
如图,AB=AD,∠BAD=∠CAE,AC=AE,求证:BC=DE.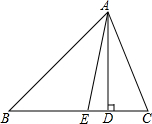 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.