题目内容
已知正五边形ABCDE内接于⊙O,点P为
的中点,求证:PA与⊙O的半径的和等于PC.
 |
| AB |
考点:正多边形和圆
专题:证明题
分析:首先根据题意画出图形,然后连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.易求得△OPA是等腰三角形,继而求得∠CPO=∠POA,∠POC=∠OPQ=108°,证得PC∥OQ,OC∥PQ,可得四边形OCPQ是平行四边形,即可证得结论.
解答: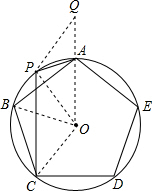 证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.
证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.
∵五边形ABCDE是正五边形,
∴∠AOB=∠BOC=
=72°,
∵点P为
的中点,
∵∠POA=∠POB=
∠AOB=36°,
∴∠PAO=∠APO=
(180°-36°)=72°,
∵AP=AQ,
∴∠PQA=∠APQ=
∠PAO=
×72°=36°,
∴∠PQA=∠POA,
∴PQ=PO.
∵∠POC=∠BOC+∠POB=72°+36°=108°,OP=OC,
∴∠CPO=∠PCO=
(180°-108°)=36°,
∴∠CPO=∠POA,∠POC=∠OPQ=108°,
∴PC∥OQ,OC∥PQ,
∴四边形OCPQ是平行四边形,
∴PC=OQ=OA+AQ=OA+PA.
即PA与⊙O的半径的和等于PC.
 证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.
证明:连接OA并延长至Q,使得AQ=PA;连接OP、OC、OB.∵五边形ABCDE是正五边形,
∴∠AOB=∠BOC=
| 360° |
| 5 |
∵点P为
 |
| AB |
∵∠POA=∠POB=
| 1 |
| 2 |
∴∠PAO=∠APO=
| 1 |
| 2 |
∵AP=AQ,
∴∠PQA=∠APQ=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PQA=∠POA,
∴PQ=PO.
∵∠POC=∠BOC+∠POB=72°+36°=108°,OP=OC,
∴∠CPO=∠PCO=
| 1 |
| 2 |
∴∠CPO=∠POA,∠POC=∠OPQ=108°,
∴PC∥OQ,OC∥PQ,
∴四边形OCPQ是平行四边形,
∴PC=OQ=OA+AQ=OA+PA.
即PA与⊙O的半径的和等于PC.
点评:此题考查了正多边形与圆的知识、等腰三角形的性质以及平行四边形的性质与判定.此题难度较大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
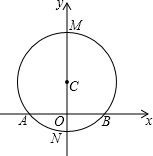 如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标
如图,AB是⊙C的弦,直径MN⊥AB于点O,MN=10,AB=8,以直线AB为x轴,直线MN为y轴建立坐标系.我们把横纵坐标都是整数的点叫做整数点,请写出⊙C上位于第二象限和第三象限的整数点的坐标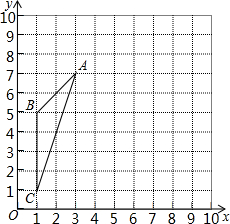 如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,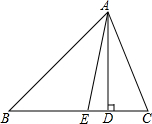 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.
如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=5°,∠B=50°,求∠C的度数.