题目内容
已知函数y=kx2-7x-7的图象和x轴有交点，则k的取值范围是__________
【解析】【解析】
分两种情况讨论：①若k=0，则y=-7x-7是一次函数，与x轴有交点；
②若k≠0，则函数y=kx2-7x-7是二次函数．∵二次函数y=kx2﹣7x﹣7的图象和x轴有交点，∴，∴k≥且k≠0．
综上所述：k≥．故答案为：k≥．
名校课堂系列答案等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中，一定是轴对称图形的有（ ）
A. 3个 B. 4个 C. 5个 D. 2个
A
【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形，是轴对称图形的有3个.
故选：A. 扎西的爷爷用一段长30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
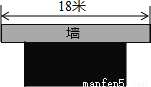
当矩形的长为15m，宽为7.5m时，矩形菜园的面积最大，最大面积为112.5m2
【解析】试题分析：设菜园宽为x，则长为36-2x，由面积公式写出y与x的函数关系式，然后利用二次函数的最值的知识可得出菜园的最大面积，及取得最大面积时矩形的长和宽．
设长为x米，宽为(30-x)/2米-,面积为y米2
当x=15时，y最大=112.5
答：最大面积是112.5米2． 如图所示是二次函数y=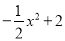
的图象在x轴上方的一部分，对于这段图象与x轴所围成的阴影部分的面积，你认为可能的值是（ ）
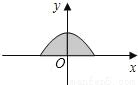
A. 4 B.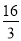 
C. 2π D. 8
B
【解析】函数与y轴交于（0，2）点，与x轴交于（-2，0）和（2，0）两点，则三点构成的三角形面积S1=4，则以半径为2的半圆的面积为S2=π××22=2π，则阴影部分的面积S有：4＜S＜2π．因为选项A、C、D均不在S取值范围内．故选 B 如果一个二次函数的图象经过点A(6，10)，与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，且x1＋x2＝6，x1x2＝5，求这个二次函数的解析式．
解析式为y＝2x2－12x＋10．
【解析】试题分析：设交点式为y=a（x﹣x1）（x﹣x2），再展开合并后把x1+x2=6，x1x2=5代入可得y=a（x2﹣6x+5），然后把A点坐标代入求出a的值即可．
试题解析：【解析】
∵抛物线与x轴交于B，C两点，点B，C的横坐标分别为x1，x2，∴抛物线解析式可设为y=a（x﹣x1）（x﹣x2）=a[x2﹣（x1+x2）x+x1x2]，而... 函数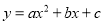
的图象如图所示，则下列结论错误的是（ ）
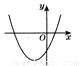
A. a＞0 B. b2－4ac＞0
C.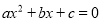 
的两根之和为负 D. 
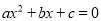的两根之积为正
D
【解析】【解析】
∵抛物线开口向上，∴a＞0，故A正确．
∵抛物线与x轴有两个交点，∴b2－4ac＞0，故B正确．
由图象可知， 一根为正，一根为负，且负根的绝对值大于正根的绝对值，∴两根之和为负，两根之积为负，故C正确，D错误．
故选D． 某商场要经营一种新上市的文具，进价为20元，试营销阶段发现：当销售单价是25元时，每天的销售量为250件，销售单价每上涨1元，每天的销售量就减少10件．
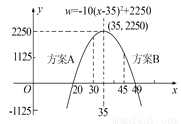
(1)写出商场销售这种工具，每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式；
(2)求销售单价为多少元时，该文具每天的销售利润最大；
(3)商场的营销部结合上述情况，提出了A、B两种营销方案：
方案A：该文具的销售单价高于进价且不超过30元；
方案B：每天销售量不少于10件，且每件文具的利润至少为25元．
请比较哪种方案的最大利润更高，并说明理由．
（1）w＝－10x2＋700x－10000；
（2）销售单价为35元时，每天销售利润最大，最大利润为2250元；
（3）方案A的最大利润更高，理由见解析.
【解析】试题分析：（1）根据利润=（销售单价-进价）×销售量，列出函数关系式即可；
（2）根据（1）式列出的函数关系式，运用配方法求最大值；
（3）分别求出方案A、B中x的取值范围，然后分别求出A、B方案的最大利润... 二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，若|ax2＋bx＋c|＝k(k≠0)有两个不相等的实数根，则k的取值范围是( )
A. k＜－3 B. k＞－3 C. k＜3 D. k＞3
D
【解析】试题分析：∵当ax2+bx+c≥0，y=ax2+bx+c（a≠0）的图象在x轴上方，
∴此时y=|ax2+bx+c|=ax2+bx+c，
∴此时y=|ax2+bx+c|的图象是函数y=ax2+bx+c（a≠0）在x轴上方部分的图象，
∵当ax2+bx+c＜0时，y=ax2+bx+c（a≠0）的图象在x轴下方，
∴此时y=|ax2+bx+c|=﹣（ax2+b... 某厂今年一月份新产品的研发资金为a元，以后每月新产品的研发资金与上月相比增长率都是x，则该厂今年三月份新产品的研发资金y(元)关于x的函数关系式为____．
y＝a(1＋x)2
【解析】试题分析：∵一月份新产品的研发资金为a元，
2月份起，每月新产品的研发资金与上月相比增长率都是x，
∴2月份研发资金为，∴三月份的研发资金为．
故答案为： ．