��Ŀ����
���һ�����κ�����ͼ����A(6��10)����x�ύ��B��C���㣬��B��C�ĺ�����ֱ�Ϊx1��x2����x1��x2��6��x1x2��5����������κ����Ľ���ʽ��
 ����ʽΪy��2x2��12x��10��
������������������轻��ʽΪy=a��x��x1����x��x2������չ���ϲ����x1+x2=6��x1x2=5����ɵ�y=a��x2��6x+5����Ȼ���A������������a��ֵ���ɣ�
�����������������
����������x�ύ��B��C���㣬��B��C�ĺ�����ֱ�Ϊx1��x2���������߽���ʽ����Ϊy=a��x��x1����x��x2��=a[x2����x1+x2��x+x1x2]����...
����ʽΪy��2x2��12x��10��
������������������轻��ʽΪy=a��x��x1����x��x2������չ���ϲ����x1+x2=6��x1x2=5����ɵ�y=a��x2��6x+5����Ȼ���A������������a��ֵ���ɣ�
�����������������
����������x�ύ��B��C���㣬��B��C�ĺ�����ֱ�Ϊx1��x2���������߽���ʽ����Ϊy=a��x��x1����x��x2��=a[x2����x1+x2��x+x1x2]����...
 ���ٴ�����ɽ����ϵ�д�
���ٴ�����ɽ����ϵ�д���ABC�У�AB =AC����D��AC�ϣ���BD =BC =AD�����A���ڣ� ��
A. 30�� B. 45�� C. 36�� D. 72��
 C
�����������кܶ���������Σ�
��õ��ܶ�ԳƵ�ͼ�Σ�
��������⽫��ͼ�������������ͼ��ʾ��
���A=36��
��ѡ��C
C
�����������кܶ���������Σ�
��õ��ܶ�ԳƵ�ͼ�Σ�
��������⽫��ͼ�������������ͼ��ʾ��
���A=36��
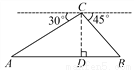
��ѡ��C ��ͼ����������C����õ���A��B����ĸ��Ƿֱ���30�㡢45��.�����ʱ������C���ĸ߶�CDΪ100�ף���A��D��B��ͬһֱ���ϣ���AB����ľ�����( )
A. 200�� B. 200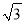 �� C. 220
�� C. 220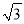 �� D. 100(
�� D. 100(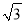 ��1)��
��1)��
 D
���������������������ƽ���ߵ����ʿɵã���A=30�㣬��B=45�㣮��Rt��ACD�У�tan��A=tan30��=����AD=�ף���Rt��CDB�У�tan��B=tan45��=����AD=100�ף���AB=AD+BD=100(+1)�ף�ѡD��
D
���������������������ƽ���ߵ����ʿɵã���A=30�㣬��B=45�㣮��Rt��ACD�У�tan��A=tan30��=����AD=�ף���Rt��CDB�У�tan��B=tan45��=����AD=100�ף���AB=AD+BD=100(+1)�ף�ѡD�� ����������Ϊ70Ԫ��ij����Ʒ�����ۼ�100Ԫһ���۳�ʱ��ÿ��������20������������Ʒ�����ۼ�ÿ����1Ԫ����������������1����Ϊ�˻�ȡÿ�����������Ӧ���ۣ� ��
A. 5Ԫ B. 10Ԫ C. 15Ԫ D. 20Ԫ
 A
����������Ӧ����xԪ��������ΪyԪ����������ɵã�
��
�����䷽�ã�
��
�൱ʱ��y���=625��
�� B��C��D����ѡA.
A
����������Ӧ����xԪ��������ΪyԪ����������ɵã�
��
�����䷽�ã�
��
�൱ʱ��y���=625��
�� B��C��D����ѡA. ��һ����Ϊ50 cm����˿���һ�������Σ�����������ε�һ�߳�Ϊx��cm�����������Ϊy��cm2������y��x֮��ĺ�����ϵʽΪ��������
A. y����x2��50x B. y��x2��50x C. y����x2��25x D. y����2x2��25
 C
������������������ε�һ�߳�Ϊxcm������һ�߳�Ϊ��25-x��cm�����ݳ����ε������ʽ�ɵ�y=x��25-x��=��x2��25x����ѡC.
C
������������������ε�һ�߳�Ϊxcm������һ�߳�Ϊ��25-x��cm�����ݳ����ε������ʽ�ɵ�y=x��25-x��=��x2��25x����ѡC. ��֪����y=kx2-7x-7��ͼ���x���н��㣬��k��ȡֵ��Χ��__________
 ����������������
������������ۣ�����k=0����y=-7x-7��һ�κ�������x���н��㣻
����k��0������y=kx2-7x-7�Ƕ��κ������߶��κ���y=kx2��7x��7��ͼ���x���н��㣬�࣬��k����k��0��
����������k�ݣ��ʴ�Ϊ��k�ݣ�
����������������
������������ۣ�����k=0����y=-7x-7��һ�κ�������x���н��㣻
����k��0������y=kx2-7x-7�Ƕ��κ������߶��κ���y=kx2��7x��7��ͼ���x���н��㣬�࣬��k����k��0��
����������k�ݣ��ʴ�Ϊ��k�ݣ� ����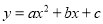 ��ͼ����ͼ����ô����x�ķ���
��ͼ����ͼ����ô����x�ķ���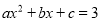 �ĸ�������ǣ� ��
�ĸ�������ǣ� ��
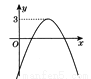
A. ����������ȵ�ʵ���� B. ���������ʵ����
C. ���������ʵ���� D. ��ʵ����
 C
����������������
������y=ax2+bx+c��ͼ������ƽ��3����λ���ɵó�����y=ax2+bx+c��3��ͼ�ߺ���y=ax2+bx+c��ͼ�����£�����������Ϊ3���ຯ��y=ax2+bx+c��3��ͼ����x��ֻ��һ�����㣬���ax2+bx+c��3=0��������ȵ�ʵ������
�ʴ�Ϊ������ax2+bx+c��3=0��������ȵ�ʵ������
C
����������������
������y=ax2+bx+c��ͼ������ƽ��3����λ���ɵó�����y=ax2+bx+c��3��ͼ�ߺ���y=ax2+bx+c��ͼ�����£�����������Ϊ3���ຯ��y=ax2+bx+c��3��ͼ����x��ֻ��һ�����㣬���ax2+bx+c��3=0��������ȵ�ʵ������
�ʴ�Ϊ������ax2+bx+c��3=0��������ȵ�ʵ������ ���κ���y��x2��(m��4)x��m��ͼ����x��������������y��Գƣ����䶥������Ϊ___________��
 (0����4)
�����������ݶ��κ���y��x2��(m��4)x��m��ͼ����x��������������y��Գƣ���֪�����߹���y��Գƣ����� =0�����m=4��������Ϊ��0��-4����
�ʴ�Ϊ����0��-4��.
(0����4)
�����������ݶ��κ���y��x2��(m��4)x��m��ͼ����x��������������y��Գƣ���֪�����߹���y��Գƣ����� =0�����m=4��������Ϊ��0��-4����
�ʴ�Ϊ����0��-4��. ��֪����y��(m2��4)x2��(m2��3m��2)x��m��1��
(1)��mΪ��ֵʱ��y��x�Ķ��κ���?
(2)��mΪ��ֵʱ��y��x��һ�κ���?
 (1) m�١�2����2��m����2
�������������������1�����ݶ��κ����ĸ���������ϵ����Ϊ0���Ա�������ߴ���Ϊ2����⼴�ɣ�
��2������һ�κ����ĸ��һ����ϵ����Ϊ0���������ϵ��Ϊ0����ʽ��⼴��.
���������(1)��m2��4��0�����m�١�2���ʵ�m�١�2ʱ��y��x�Ķ��κ�����
(2)��m2��4��0�����m=��2����m2��3m��2��0�����m��1��m��2������m...
(1) m�١�2����2��m����2
�������������������1�����ݶ��κ����ĸ���������ϵ����Ϊ0���Ա�������ߴ���Ϊ2����⼴�ɣ�
��2������һ�κ����ĸ��һ����ϵ����Ϊ0���������ϵ��Ϊ0����ʽ��⼴��.
���������(1)��m2��4��0�����m�١�2���ʵ�m�١�2ʱ��y��x�Ķ��κ�����
(2)��m2��4��0�����m=��2����m2��3m��2��0�����m��1��m��2������m... 
