��Ŀ����
������үү��һ�γ�30m�����Χ��һ��һ�߿�ǽ�ľ��β���ǽ��Ϊ18m��������εij�������Ϊ����ʱ�������������������Ƕ��٣�
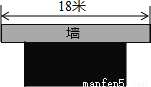
 �����εij�Ϊ15m����Ϊ7.5mʱ�����β���������������Ϊ112.5m2
����������������������Ϊx����Ϊ36-2x���������ʽд��y��x�ĺ�����ϵʽ��Ȼ�����ö��κ�������ֵ��֪ʶ�ɵó���������������ȡ��������ʱ���εij��Ϳ���
�賤Ϊx�ף���Ϊ(30-x)/2��-,���Ϊy��2
��x=15ʱ��y���=112.5
����������112.5��2��
�����εij�Ϊ15m����Ϊ7.5mʱ�����β���������������Ϊ112.5m2
����������������������Ϊx����Ϊ36-2x���������ʽд��y��x�ĺ�����ϵʽ��Ȼ�����ö��κ�������ֵ��֪ʶ�ɵó���������������ȡ��������ʱ���εij��Ϳ���
�賤Ϊx�ף���Ϊ(30-x)/2��-,���Ϊy��2
��x=15ʱ��y���=112.5
����������112.5��2��
�����㣺7.292��2.712=__��
 45.8
��������7.292��2.712=(7.29+2.71)(7.29-2.71)=10��4.58=45.8.
45.8
��������7.292��2.712=(7.29+2.71)(7.29-2.71)=10��4.58=45.8. �÷�֤��֤�����⡰�Զ�����ȡ���һ������__________________.
 �Զ��Dz����
��������������������÷�֤��������֤��ʱ�����ȼ�����۲����������ȼ��衰�Զ��Dz���ȡ���
�Զ��Dz����
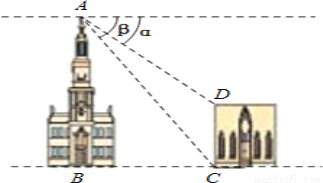
��������������������÷�֤��������֤��ʱ�����ȼ�����۲����������ȼ��衰�Զ��Dz���ȡ��� ��ͼ�����������ˮƽ����BCΪ18m����A����D��ĸ��Ǧ�Ϊ30�㣬���C��ĸ��Ǧ�Ϊ60�㣮������CD�ĸ߶�Ϊ m������������Ƽ��㣩��
 ��������
�������������D��DE��AB�ڵ�E��
���ı���BCDE�Ǿ��Σ�
��������ã���ACB=��=60�㣬��ADE=��=30�㣬BC=18m��
��DE=BC=18m��CD=BE��
��Rt��ABC�У�AB=BC•tan��ACB=18��tan60��=18��m����
��Rt��ADE�У�AE=DE•tan��ADE=18��tan30��=6��m����
��DC=BE=AB...
��������
�������������D��DE��AB�ڵ�E��
���ı���BCDE�Ǿ��Σ�
��������ã���ACB=��=60�㣬��ADE=��=30�㣬BC=18m��
��DE=BC=18m��CD=BE��
��Rt��ABC�У�AB=BC•tan��ACB=18��tan60��=18��m����
��Rt��ADE�У�AE=DE•tan��ADE=18��tan30��=6��m����
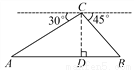
��DC=BE=AB... ��ͼ����������C����õ���A��B����ĸ��Ƿֱ���30�㡢45��.�����ʱ������C���ĸ߶�CDΪ100�ף���A��D��B��ͬһֱ���ϣ���AB����ľ�����( )
A. 200�� B. 200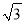 �� C. 220
�� C. 220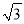 �� D. 100(
�� D. 100(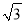 ��1)��
��1)��
 D
���������������������ƽ���ߵ����ʿɵã���A=30�㣬��B=45�㣮��Rt��ACD�У�tan��A=tan30��=����AD=�ף���Rt��CDB�У�tan��B=tan45��=����AD=100�ף���AB=AD+BD=100(+1)�ף�ѡD��
D
���������������������ƽ���ߵ����ʿɵã���A=30�㣬��B=45�㣮��Rt��ACD�У�tan��A=tan30��=����AD=�ף���Rt��CDB�У�tan��B=tan45��=����AD=100�ף���AB=AD+BD=100(+1)�ף�ѡD�� ��ͼ����֪��P�İ뾶Ϊ2��Բ��P��������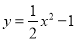 ���˶�������P��x������ʱ��Բ��P������Ϊ_____________
���˶�������P��x������ʱ��Բ��P������Ϊ_____________
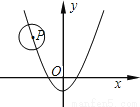
 ����2����2��
����������������������⣬����P��x��2����P��x����2����
�ٵ�P�������ǣ�x��2��ʱ���������y=x2��1����
2=x2��1��
���x=����
��ʱP����2������2����
�ڵ�P�������ǣ�x����2��ʱ���������y=x2��1����
��2=x2��1������1=x2
�⣮
�������������������ĵ�P�������ǣ���2������2��
����2����2��
����������������������⣬����P��x��2����P��x����2����
�ٵ�P�������ǣ�x��2��ʱ���������y=x2��1����
2=x2��1��
���x=����
��ʱP����2������2����
�ڵ�P�������ǣ�x����2��ʱ���������y=x2��1����
��2=x2��1������1=x2
�⣮
�������������������ĵ�P�������ǣ���2������2�� ����������Ϊ70Ԫ��ij����Ʒ�����ۼ�100Ԫһ���۳�ʱ��ÿ��������20������������Ʒ�����ۼ�ÿ����1Ԫ����������������1����Ϊ�˻�ȡÿ�����������Ӧ���ۣ� ��
A. 5Ԫ B. 10Ԫ C. 15Ԫ D. 20Ԫ
 A
����������Ӧ����xԪ��������ΪyԪ����������ɵã�
��
�����䷽�ã�
��
�൱ʱ��y���=625��
�� B��C��D����ѡA.
A
����������Ӧ����xԪ��������ΪyԪ����������ɵã�
��
�����䷽�ã�
��
�൱ʱ��y���=625��
�� B��C��D����ѡA. ��֪����y=kx2-7x-7��ͼ���x���н��㣬��k��ȡֵ��Χ��__________
 ����������������
������������ۣ�����k=0����y=-7x-7��һ�κ�������x���н��㣻
����k��0������y=kx2-7x-7�Ƕ��κ������߶��κ���y=kx2��7x��7��ͼ���x���н��㣬�࣬��k����k��0��
����������k�ݣ��ʴ�Ϊ��k�ݣ�
����������������
������������ۣ�����k=0����y=-7x-7��һ�κ�������x���н��㣻
����k��0������y=kx2-7x-7�Ƕ��κ������߶��κ���y=kx2��7x��7��ͼ���x���н��㣬�࣬��k����k��0��
����������k�ݣ��ʴ�Ϊ��k�ݣ� ��ͼ��ʾ��һˮ��ӭˮ��AB���¶�i=1��2�����½Ǧ�������ֵsin��
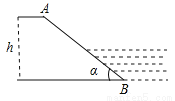
 ��������������������ȹ���A��AC��BC�ڵ�C����AC=x������AC=x�������±ȿɵ�BC=2x�����ݹ��ɶ������AB�ij��ȣ�Ȼ��������ҵ��ó��𰸣�
�����������A��AC��BC��C�� ��AB���¶�i=1��2��
��tan��=�� ��AC=x��BC=2x�� ���ݹ��ɶ����ɵã�AB= ��
��sin��=��
��������������������ȹ���A��AC��BC�ڵ�C����AC=x������AC=x�������±ȿɵ�BC=2x�����ݹ��ɶ������AB�ij��ȣ�Ȼ��������ҵ��ó��𰸣�
�����������A��AC��BC��C�� ��AB���¶�i=1��2��
��tan��=�� ��AC=x��BC=2x�� ���ݹ��ɶ����ɵã�AB= ��
��sin��=�� 
