题目内容
6.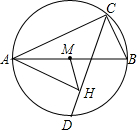 如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )
如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )| A. | 1 | B. | 1.5 | C. | 0.5 | D. | 0.7 |
分析 延长HM交AC于K,首先证明△AHC是等腰直角三角形,再证明点M是圆心,求出HK、MK即可解决问题.
解答 解:延长HM交AC于K.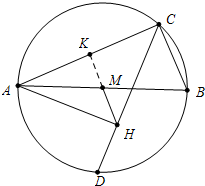 ∵AB是直径,
∵AB是直径,
∴∠ACB=90°
∵$\widehat{AD}$=$\widehat{BD}$,
∴∠ACD=∠BCD=45°,
∵AH⊥CD,
∴∠AHC=90°,
∴∠HAC=∠HCA=45°,
∴HA=HC,
∵HM平分∠AHC,
∴HK⊥AC,AK=KC
∴点M就是圆心,
∵AK=KC,AM=MB,
∴KM=$\frac{1}{2}$BC=$\frac{1}{2}$,
在RT△ACH中,∵AC=3,AK=KC,∠AHC=90°,
∴HK=$\frac{1}{2}$AC=$\frac{3}{2}$,
∴HM=HK-KM=$\frac{3}{2}$-$\frac{1}{2}$=1.
故选A.
点评 本题考查垂径定理、三角形中位线定理、圆周角定理等知识,解题的关键是证明点M是圆心,属于中考常考题型.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
17.关于x的方程x2-mx+2=0的两根和是3,两根积是2,则m的值是( )
| A. | -3 | B. | 3 | C. | 2 | D. | -2 |
1.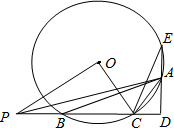 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
 如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E
如图,△ABC内接于⊙O,AD⊥BC于D交⊙O于E(1)若∠ACB=120°,求证:CE=⊙O的半径.
(2)连OC,OP⊥OC交CB的延长线于P,若⊙O的半径为5cm,弦BC=6cm,求PB的长.
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
16. 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
 如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )
如图,设数轴上的点A,B,C表示的数分别为a,b,c,则下列说法中错误的是( )| A. | a<0 | B. | b>0 | C. | c>b | D. | a-b>0 |
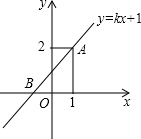 如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).
如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P是坐标轴上的一点,且满足∠APB=90°,则点P的坐标是P1(1,0),P2(0,1+$\sqrt{2}$),P3(0,1-$\sqrt{2}$).