题目内容
15. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )
如图,AB是⊙O的一条弦,点C是⊙O上一动点,且AB=4,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为5,当GE+FH的值最大时,弦BC的长等于( )| A. | 8 | B. | 10 | C. | 2$\sqrt{21}$或8 | D. | 2$\sqrt{21}$或10 |
分析 根据题意得出当GH最长为直径时,GE+FH的值最大,由三角形中位线定理得出GH⊥BC,CF=BF,再根据勾股定理得出CF,从而得出弦BC的长.
解答  解:分两种情况:
解:分两种情况:
①如图1,
∵AB=4,点E、F分别为AC、BC的中点,
∴EF=2,
∴当GH最长为直径时,GE+FH的值最大,
∴GH⊥BC,
∴CF=BF,
∵OC=5,
∴CF=$\sqrt{{5}^{2}-{2}^{2}}$=$\sqrt{21}$,
∴BC=2$\sqrt{21}$;
②如图2,
∵AB=4,点E、F分别为AC、BC的中点,
∴EF=2,
∴当GH最长为直径时,GE+FH的值最大,
∴GH⊥AC,
∴CE=AE,
∵OC=5,
∴BC=10;
∴BC=10或2$\sqrt{21}$,
故选D.
点评 本题考查了三角形的中位线定理以及垂径定理,注意分类讨论思想的运用是解题的关键.

练习册系列答案
相关题目
8.为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节目的目的;该市自来水收费的价目表如下表(注:水费按月份结算)
(1)若该户居民1月份用水12.5立方米,则应该付水费多少元?
(2)若该户居民2月份缴纳水费40元,则其2月份用水量为多少立方米?
(3)若该户居民3、4月份共用水15立方米(4月份超过3月份),共交水费44元,则若该用户居民3、4月份各用水多少立方米?
| 每月用水量 | 单价 |
| 不超过6立方米 | 每立方米2元 |
| 超过6立方米不超过10立方米部分 | 每立方米4元 |
| 超出10立方米部分 | 每立方米8元 |
(2)若该户居民2月份缴纳水费40元,则其2月份用水量为多少立方米?
(3)若该户居民3、4月份共用水15立方米(4月份超过3月份),共交水费44元,则若该用户居民3、4月份各用水多少立方米?
10.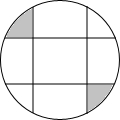 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为( )| A. | $\sqrt{2}$π | B. | 2-π | C. | π | D. | 2π |
4.将抛物线y=2x2经过怎样的平移可得到抛物线y=2(x+3)2-4( )
| A. | 先向左平移3个单位,再向上平移4个单位 | |
| B. | 先向左平移3个单位,再向下平移4个单位 | |
| C. | 先向右平移3个单位,再向上平移4个单位 | |
| D. | 先向右平移3个单位,再向下平移4个单位 |
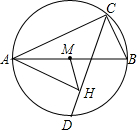 如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )
如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )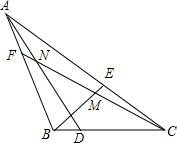 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).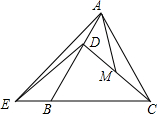 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.