题目内容
11.一次数学活动课上,两位学生小韩和小苏利用计算机软件探索函数问题,下面是他们的交流片断.如图中的(1)(2).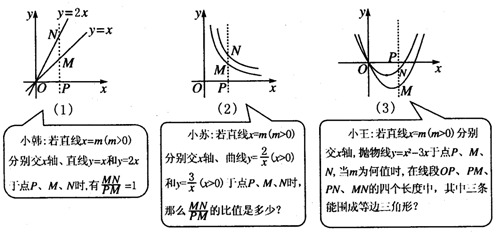
问题解决:
(1)小苏提出的问题$\frac{MN}{PM}$的比值是多少?
(2)记图①和图②中MN为d1,d2,分别求出d1,d2与m之间的函数关系式,并指出函数的增减性.
拓广探索:
(3)学生小王又提出新的问题如图③二次函数的图象,求m为何值时,OP、PM、PN、MN四个长度中,其中任意三条能围成等边三角形?
分析 (1)根据直线x=m与x轴,y=$\frac{2}{x}$,y=$\frac{3}{x}$的交点,表示出P,M,N,进而表示出|MN|与|PM|,即可求出所求之比;
(2)如图①,表示出d1与m的关系式,即可作出判断;如图②,表示出d2与m的关系式,即可作出判断;
(3)把x=m(m≠0)分别代入抛物线解析式,表示出|MN|=OP=m,分两种情况考虑:当OP=MN=PM;当OP=MN=PM,分别求出m的值即可.
解答 解:(1)∵x=m与x轴,y=$\frac{2}{x}$,y=$\frac{3}{x}$分别交于点P、M、N,
∴P点坐标为(m,0),M坐标为(m,$\frac{2}{m}$),N坐标为(m,$\frac{3}{m}$),
∴|MN|=$\frac{3}{m}$-$\frac{2}{m}$=$\frac{1}{m}$,|PM|=$\frac{2}{m}$,
则$\frac{MN}{PM}$=$\frac{\frac{1}{m}}{\frac{2}{m}}$=$\frac{1}{2}$;
(2)在图①中,|MN|=2m-m=m,即d1=m,d1随着m的增大而增大;
在图②中,|MN}=$\frac{2}{m}$-$\frac{1}{m}$=$\frac{1}{m}$,即d2=$\frac{1}{m}$,d2随m的增大而减小;
(3)由题意,把x=m(m≠0)分别代入抛物线y=x2-4x,y=x2-3x中,有|MN|=|yN-yM|=m,即MN=OP=m,
分两种情况考虑:当OP=MN=PM,即|m2-4m|=m时,解得m=3,5;
当OP=MN=PM,即|m2-3m|=m时,解得m=2,4,
综上,m=2,3,4,5.
点评 此题属于二次函数综合题,涉及的知识有:坐标与图形性质,以及二次函数的性质,熟练掌握二次函数的性质是解本题的关键.

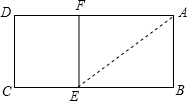 如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )
如图,已知矩形ABCD中,AB=2,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点处,若四边形EFDC与矩形ABCD相似,则AD=( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | 4 | D. | 2$\sqrt{3}$ |
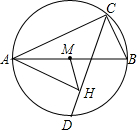 如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )
如图,已知AB为圆的直径,C为半圆上一点,D为半圆的中点,AH⊥CD,垂足为H,HM平分∠AHC,HM交AB于M.若AC=3,BC=1,则MH长为( )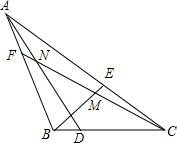 点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).
点D、E、F分别在△ABC的BC,CA,AB边上,∠CAD=3∠BAD,∠ABE=3∠CBE,∠BCF=3∠ACF,BE、CF交于点M,CF、AD交于点N,且满足∠BMF=2∠CND,那么∠BAC等于$\frac{180}{7}$(度).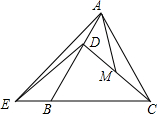 如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.
如图,等边△ABC中,点D在边AB上,E在CB的延长线上,已知CD=ED,M是CD中点,AM=2$\sqrt{2}$,则AE=4$\sqrt{2}$.