题目内容
1. (1)三角形的内角和等于180°;
(1)三角形的内角和等于180°;(2)请完成下面说明上述结论的正确性的过程,如图,已知△ABC,求证:∠A+∠B+∠C=180°.
分析 (1)三角形内角和为180°;
(2)延长BC到D,过点C作CE∥BA,根据两直线平行,同位角相等可得∠B=∠1,两直线平行,内错角相等可得∠A=∠2,再根据平角的定义列式整理即可得证.
解答 解:(1)三角形内角和为180°.故答案为:180°;
(2) 证明:如图,延长BC到D,过点C作CE∥BA,
证明:如图,延长BC到D,过点C作CE∥BA,
∵BA∥CE,
∴∠B=∠1(两直线平行,同位角相等),
∠A=∠2(两直线平行,内错角相等),
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
点评 本题考查了三角形的内角和定理的证明,作辅助线把三角形的三个内角转化到一个平角上是解题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
11.下列二次根式是最简二次根式的是( )
| A. | 2$\sqrt{a}$ | B. | $\sqrt{8{x}^{2}}$ | C. | $\sqrt{{y}^{3}}$ | D. | $\sqrt{\frac{b}{4}}$ |
12.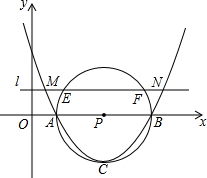 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
 如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )
如图,已知抛物线y=mx2-6mx+5m与x轴交于A、B两点,以AB为直径的⊙P经过该抛物线的顶点C,直线l∥x轴,交该抛物线于M、N两点,交⊙P与E、F两点,若EF=2$\sqrt{3}$,则MN的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{2}$ | C. | 5 | D. | 6 |
7.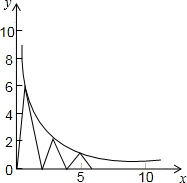 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
 如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )
如图,每个底边为2的等腰三角形顶角的顶点都在反比例函数y=$\frac{6}{x}$(x>0)的图象上,第1个等腰三角形顶角的顶点横坐标为1,第2个等腰三角形的顶点横坐标为3,…以此类推,用含n的式子表示第n个等腰三角形底边上的高为( )| A. | $\frac{6}{2n-1}$ | B. | $\frac{6}{{2}^{n+1}}$ | C. | $\frac{6}{2n+1}$ | D. | $\frac{6}{{2}^{n-1}}$ |
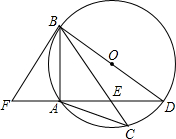 如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.
如图,在⊙O中,AB=AC,BD为直径,弦AD与BC相交于点E,延长DA到F,使∠ABF=∠ABC.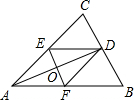 如图,AD是∠CAB的平分线,DE∥AB,DF∥AC,EF交AD于点O,请问:
如图,AD是∠CAB的平分线,DE∥AB,DF∥AC,EF交AD于点O,请问: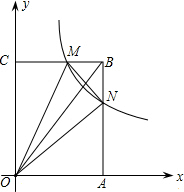 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.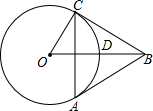 如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC.
如图,⊙O的半径为2,OB=4,OB交⊙O于点D,点C是⊙O上一动点,以BC为边向下作等边△ABC.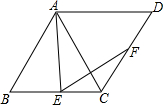 如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.
如图,菱形ABCD中,∠B=60°,点E、F分别在BC、CD边上,∠AEF=60°,求证:AE=EF.