题目内容
6.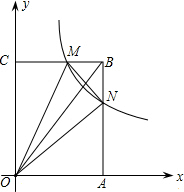 如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
如图,在平面直角坐标系中,反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,分别与矩形的BC、BA边相交于M、N,△BMN的面积等于9,则k的值为8.
分析 由四边形OABC是矩形,得到AB=OC,OA=BC,设B(a,b),根据反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,表示出E($\frac{1}{2}$a,$\frac{1}{2}$b),M($\frac{k}{b}$,b),N(a,$\frac{k}{a}$),利用△BMN的面积等于9,列方程求解.
解答 解:∵四边形OABC是矩形,
∴AB=OC,OA=BC,
设B(a,b),
∵反比例函数y=$\frac{k}{x}$在第一象限的部分经过矩形OABC的中心E,
∴E($\frac{1}{2}$a,$\frac{1}{2}$b),
∴$\frac{1}{2}$a$•\frac{1}{2}$b=k,即ab=4k,
∵M,N在反比例函数y=$\frac{k}{x}$的图象上,
∴M($\frac{k}{b}$,b),N(a,$\frac{k}{a}$),
∴BM=a-$\frac{k}{b}$,BN=b-$\frac{k}{a}$,
∴S△BMN=$\frac{1}{2}$BM•BN=$\frac{1}{2}$(a-$\frac{k}{b}$)(b-$\frac{k}{a}$)=9,
∴k=8,
故答案为:8.
点评 本题考查了用待定系数法求反比例函数的解析式、反比例函数系数k的几何意义、反比例函数图象上点的特征以及矩形的性质,理解反比例函数系数k的几何意义是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
17.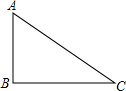 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
 △ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )
△ABC中,∠B=90°,AC=$\sqrt{5}$,tan∠C=$\frac{1}{2}$,则BC边的长为( )| A. | $2\sqrt{5}$ | B. | 2 | C. | $\sqrt{5}$ | D. | 4 |
 (1)三角形的内角和等于180°;
(1)三角形的内角和等于180°;

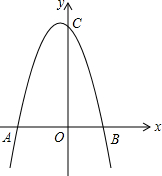 如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.
如图,抛物线y=-x2-x+6与x轴交于A、B两点,与y轴交于点C.