��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�������y=-x2+2x+3��x�ύ��A��B���㣬��y�ύ�ڵ�C����D�Ǹ������ߵĶ��㣮
��1����B��D��������꼰ֱ��AC�Ľ���ʽ��
��2��ֱ��DEΪ���������ߵĶԳ��ᣬ����ֱ��DE����һ��M��ʹ��ACM���ܳ���С�����M������ꣻ
��3����P��x���ϵ�һ�����㣬��P����ֱ��l��AC���������ڵ�Q����̽��������P����˶��������������Ƿ���ڵ�Q��ʹ�Ե�A��P��Q��CΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�

��1����B��D��������꼰ֱ��AC�Ľ���ʽ��
��2��ֱ��DEΪ���������ߵĶԳ��ᣬ����ֱ��DE����һ��M��ʹ��ACM���ܳ���С�����M������ꣻ
��3����P��x���ϵ�һ�����㣬��P����ֱ��l��AC���������ڵ�Q����̽��������P����˶��������������Ƿ���ڵ�Q��ʹ�Ե�A��P��Q��CΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д�����������ĵ�Q�����ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1����y=0���ⷽ�����A��B�����꣬�Ѻ�������ʽ�����ɶ���ʽ��ʽ�������D�����꣬����x=0�����C�����꣬Ȼ�����ô���ϵ������һ�κ�������ʽ��⼴�ɣ�
��2��������Գ�ȷ�����·�����⣬����BC����Գ���Ľ��㼴Ϊ����ĵ�M��Ȼ�����ֱ��BC�Ľ���ʽ������⼴�ɣ�
��3���ֵ�P�ڵ�Q����ߺ��ұ��������������ƽ���ı��εĶԱ�ƽ������ȣ��ӵ�A��C�������ϵ���õ�P�������ʾ����Q�����꣬Ȼ��ѵ�Q��������������߽���ʽ��⼴�ɣ�
��2��������Գ�ȷ�����·�����⣬����BC����Գ���Ľ��㼴Ϊ����ĵ�M��Ȼ�����ֱ��BC�Ľ���ʽ������⼴�ɣ�
��3���ֵ�P�ڵ�Q����ߺ��ұ��������������ƽ���ı��εĶԱ�ƽ������ȣ��ӵ�A��C�������ϵ���õ�P�������ʾ����Q�����꣬Ȼ��ѵ�Q��������������߽���ʽ��⼴�ɣ�
����⣺��1����y=0����-x2+2x+3=0��
�����ã�x2-2x-3=0��
���x1=-1��x2=3��
���ԣ���A��-1��0����B��3��0����
��y=-x2+2x+3=-��x-1��2+4��
�ඥ��D������Ϊ��1��4����
��x=0����y=3��
���ԣ���C������Ϊ��0��3����
��ֱ��AC�Ľ���ʽΪy=kx+b��
��
��
���
��
���ԣ�ֱ��AC�Ľ���ʽΪy=3x+3��
��2����A��B���ڶԳ���ֱ��x=1�Գ��ᣬ
��ֱ��BC��Գ���Ľ��㼴Ϊֱ��DE��ʹ��ACM���ܳ���С�ĵ㣬
��ֱ��BC�Ľ���ʽΪy=mx+n��
��
��
���
��
���ԣ�ֱ��BC�Ľ���ʽΪy=-x+3��
��x=1ʱ��y=-1+3=2��
���ԣ���M������Ϊ��1��2����
��3����ֱ��l��AC��
��PQ��AC��PQ=AC��
��A��-1��0����C��0��3����
�����P��������x��0����
�������Q��x���Ϸ������Q������Ϊ��x+1��3����
��ʱ��-��x+1��2+2��x+1��+3=3��
���x1=-1����ȥ����x2=1��
���ԣ���Q������Ϊ��2��3����
������Q��x���·������Q������Ϊ��x-1��-3����
��ʱ��-��x-1��2+2��x-1��+3=-3��
�����ã�x2-4x-3=0��
���x1=2+
��x2=2-
��
���ԣ���Q������Ϊ��1+
��-3����1-
��-3����
������������Q��������2��3����1+
��-3����1-
��-3����
�����ã�x2-2x-3=0��
���x1=-1��x2=3��
���ԣ���A��-1��0����B��3��0����
��y=-x2+2x+3=-��x-1��2+4��
�ඥ��D������Ϊ��1��4����
��x=0����y=3��
���ԣ���C������Ϊ��0��3����
��ֱ��AC�Ľ���ʽΪy=kx+b��
��
|
���
|
���ԣ�ֱ��AC�Ľ���ʽΪy=3x+3��
��2����A��B���ڶԳ���ֱ��x=1�Գ��ᣬ
��ֱ��BC��Գ���Ľ��㼴Ϊֱ��DE��ʹ��ACM���ܳ���С�ĵ㣬
��ֱ��BC�Ľ���ʽΪy=mx+n��
��
|
���
|
���ԣ�ֱ��BC�Ľ���ʽΪy=-x+3��
��x=1ʱ��y=-1+3=2��
���ԣ���M������Ϊ��1��2����
��3����ֱ��l��AC��
��PQ��AC��PQ=AC��
��A��-1��0����C��0��3����
�����P��������x��0����
�������Q��x���Ϸ������Q������Ϊ��x+1��3����
��ʱ��-��x+1��2+2��x+1��+3=3��
���x1=-1����ȥ����x2=1��
���ԣ���Q������Ϊ��2��3����
������Q��x���·������Q������Ϊ��x-1��-3����
��ʱ��-��x-1��2+2��x-1��+3=-3��
�����ã�x2-4x-3=0��
���x1=2+
| 7 |
| 7 |
���ԣ���Q������Ϊ��1+
| 7 |
| 7 |
������������Q��������2��3����1+
| 7 |
| 7 |
�����������Ƕ��κ����ۺ����ͣ���Ҫ��������������x��Ľ������⣬����ϵ��������κ�������ʽ����Գ�ȷ�����·�����⣬ƽ���ı��εĶԱ�ƽ������ȵ����ʣ���2��ȷ������M��λ���ǽ���Ĺؼ�����3���ѵ����ڷ�������ۣ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
���������ε�һ������48�㣬����һ���ǵĶ����ǣ�������
| A��48�� |
| B��48���42�� |
| C��42���66�� |
| D��48���66�� |
���е�������Ҫ���ղ���ǣ�������
| A���˽�һ���ڵ������о��� |
| B������ȫ����ѧ����������� |
| C�����ij�����еĴ����� |
| D������ij��ũ����ij��� |
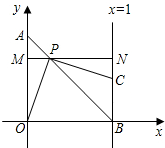 ��ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B����Ϊ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N����AP=x����PBC�����ΪS��
��ͼ����OΪԭ���ֱ������ϵ�У�A�������Ϊ��0��1����ֱ��x=1��x���ڵ�B����Ϊ�߶�AB��һ���㣬��ֱ��PC��PO����ֱ��x=1�ڵ�C����P����ֱ��MNƽ����x�ᣬ��y���ڵ�M����ֱ��x=1�ڵ�N����AP=x����PBC�����ΪS��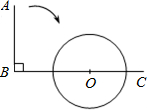 ��ͼ����ABC=90�㣬OΪ����BC��һ�㣬�Ե�OΪԲ�ģ�
��ͼ����ABC=90�㣬OΪ����BC��һ�㣬�Ե�OΪԲ�ģ�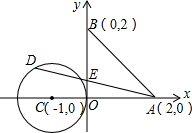 ��ͼ����֪A��B���������ֱ�Ϊ��2��0������0��2������C��Բ������Ϊ��-1��0�����뾶Ϊ1����D�ǡ�C�ϵ�һ�����㣬�߶�DA��y�ύ�ڵ�E�����ABE�������Сֵ�Ƕ��٣���д������̣�
��ͼ����֪A��B���������ֱ�Ϊ��2��0������0��2������C��Բ������Ϊ��-1��0�����뾶Ϊ1����D�ǡ�C�ϵ�һ�����㣬�߶�DA��y�ύ�ڵ�E�����ABE�������Сֵ�Ƕ��٣���д������̣�